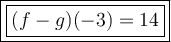Question

Need Help?

Submit Answer
3. [0/1 Points]
Need Help?
Read It
Submit Answer
DETAILS
Evaluate the indicated function for f(x) = x2 - 1 and g(x) = x - 3 algebraically. If possible, use a graphing L
(f - g)(-3)
Read It
PREVIOUS ANSWERS
Viewing Saved Work Revert to Last Response
LARPRECALCRMRP7 1.5.020.
DETAILS
4. [-/1 Points]
Evaluate the indicated function for f(x) = x² - 2 and g(x) = x - 3 algebraically. If possible, use a graphing u
(f + g)(1)
LARPRECALCRMRP7 1.5.022.

Answer 1

14

Explanation:

A composite function is formed when one function is applied to the result of another function. In this case, (f - g)(x) is formed by subtracting the function g(x) from the function f(x).

Therefore, to find (f - g)(-3), we need to subtract function g(x) from function f(x) and then evaluate the result at x = -3.

Given functions:

`f(x)=x^2-1`

`g(x)=x-3`

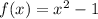
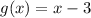
Calculate f(x) - g(x):

`\begin{aligned}(f-g)(x)&=f(x)-g(x)\\&=(x^2-1)-(x-3)\\&=x^2-1-x+3\\&=x^2-x+2\end{aligned}`

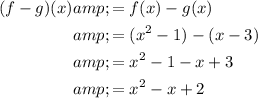
Now, substitute x = -3 into the expression:

`\begin{aligned}(f - g)(-3) &= (-3)^2 - (-3)+2\\&=9+3+2\\&=12+2\\&=14\end{aligned}`

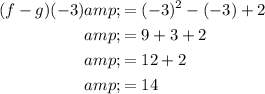
Therefore:

`\large\boxed{\boxed{(f-g)(-3)=14}}`