Question

A town has a population of 15000 and grows at 3.5% every year. To the nearest year how long will it be until the population will reach 24300 ?

Answer 1

It will take approximately 20 years for the town's population to reach 24,300.

Step-by-step explanation:

The population growth can be calculated using the formula for compound interest:
`\(A = P(1 + r/n)^(nt)\)`, where:

-
`\(A\)` is the future value of the investment/loan, which is 24,300 in this case.

-
`\(P\)` is the principal amount (the initial population), which is 15,000.

-
`\(r\)` is the annual interest rate (growth rate), expressed as a decimal, which is 3.5% or 0.035.

-
`\(n\)` is the number of times that interest is compounded per unit
`\(t\)`, which is 1 since the growth is annual.

-
`\(t\)` is the time the money is invested or borrowed for, in years.

We need to solve for
`\(t\)`, the time it takes for the population to reach 24,300. Rearranging the formula to solve for
`\(t\)`, we get:

`\[ t = (\log(A/P))/(n \cdot \log(1 + r/n)) \]`

Substituting the given values into the formula:

`\[ t = (\log(24,300/15,000))/(1 \cdot \log(1 + 0.035)) \]`

After solving this expression, we find that
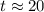`\(t \approx 20\)` years. Therefore, it will take approximately 20 years for the town's population to reach 24,300.

Answer 2

The nearest year, it will take approximately 28 years for the population to reach 24,300.

Step-by-step explanation:

To find out how long it will take for the population to reach 24,300, we can use the formula for compound interest: A = P(1 + r)^t

Where

A is the final amount

P is the initial amount

r is the growth rate

t is the time in years.

In this case, the initial population is 15,000, the growth rate is 3.5% (or 0.035 as a decimal), and we want to find out the time it takes to reach 24,300.

We can set up the equation as: 24,300 = 15,000(1 + 0.035)^t.

Simplifying the equation, we have: 1.62 = (1.035)^t.

Taking the logarithm of both sides, we get: t * ln(1.035) = ln(1.62).

Using a calculator, we find that ln(1.035) ≈ 0.034. Dividing both sides of the equation by 0.034, we get: t ≈ ln(1.62) / 0.034 ≈ 28.33.

So therefore it will take approximately 28 years for the population to reach 24,300.