Question

An electric drill starts from rest and rotates with a constant angular acceleration. After the drill has rotated through a certain angle, the magnitude of the centripetal acceleration of a point on the drill is 8.2 times the magnitude of the tangential acceleration. What is the angle?

Answer 1

The angle is 4.1 rad.

Step-by-step explanation:

The centripetal acceleration (α) is given by:

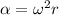`\alpha = \omega^(2) r` (1)

Where:

ω: is the angular velocity

r: is the radius

And the tangential acceleration (a) is:

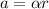`a = \alpha r` (2)

Since the magnitude of "α" is 8.2 times the magnitude of "a" (equating (2) and (1)) we have:

`\omega^(2) r = 8.2\alpha r`

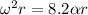
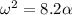`\omega^(2) = 8.2\alpha` (3)

Now, we can find the angle with the following equation:

`\omega_(f)^(2) = \omega_(0)^(2) + 2\alpha \Delta \theta`

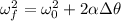
Where:

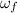`\omega_(f)`: is the final angular velocity
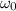`\omega_(0)`: is the initial angular velocity = 0 (it starts from rest)

`\Delta \theta`: is the angle

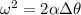`\omega^(2) = 2\alpha \Delta \theta` (4)

By entering equation (3) into (4) we can calculate the angle:

`8.2\alpha = 2\alpha \Delta \theta`

`\Delta \theta = 4.1 rad`

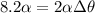
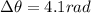
Therefore, the angle is 4.1 rad.

I hope it helps you!