Question

Watch help video Express (81^((1)/(2)))^(5) in simplest radical form

Answer 1

The expression
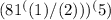`(81^((1)/(2)))^(5)` simplifies to 9^(5) according to the mathematical rule
`(a^(m))^n=a^(m*n)`. Therefore, its simplest radical form is 9^(5).

Step-by-step explanation:

To express the expression
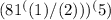`(81^((1)/(2)))^(5)` in simplest radical form, first, you must understand the basic mathematical rule:
`(a^(m))^n=a^(m*n)`.

So, the expression can be simplified as follows:

1. Express 81 as (9^2)
2. Substitute 81 in the original equation:
   `((9^2)^((1)/(2)))^(5)`
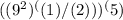
3. Use the mathematical rule
   `(a^(m))^n=a^(m*n)` and simplify:
   `9^(2*(1/2)*5)`
4. Further simplify the equation:
   `9^(5)`

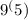
So,
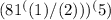`(81^((1)/(2)))^(5)` in simplest radical form is
`9^(5)`.

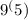Learn more about Simplifying Radicals