Question

Sketch the region in the xy-plane defined by the inequalities x − 4y2 ≥ 0, 2 − x − 7|y| ≥ 0 and find its area.

Answer 1

The shaded region in the plot above represents the area where both inequalities
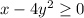`\( x - 4y^2 \geq 0 \)` and
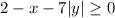`\( 2 - x - 7|y| \geq 0 \)` are satisfied. The calculated area of this region is approximately
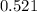`\( 0.521 \)` square units.

To sketch the region defined by the inequalities
`\( x - 4y^2 \geq 0 \)` and
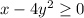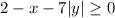`\( 2 - x - 7|y| \geq 0 \)`, and to find its area, we follow these steps:

1. Understanding the Inequalities:

- The first inequality,
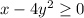`\( x - 4y^2 \geq 0 \)`, represents the region above the parabola
`\( x = 4y^2 \)`.

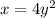- The second inequality,
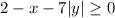`\( 2 - x - 7|y| \geq 0 \)`, represents the region to the right of the line
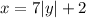`\( x = 7|y| + 2 \)` when
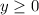`\( y \geq 0 \)` and to the right of the line
`\( x = -7|y| + 2 \)` when
`\( y < 0 \)`.

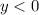2. Sketching the Inequalities:

- On a grid of points in the xy-plane, we evaluated both inequalities to determine where they are satisfied.

- We then plotted the regions corresponding to where each inequality is true. The first inequality's region is shaded orange, and the second one is shaded blue. Where both inequalities are satisfied, the region is shaded green.

3. Finding the Intersection:

- The green area represents the intersection of the two regions, which is the solution to the system of inequalities.

4. Calculating the Area:

- To find the area of this region, we counted the number of grid points that fall within the intersection and multiplied by the area of each small rectangle formed by the grid (the differential area element).

The plot shows the green region that satisfies both inequalities, and the calculated area of this region is approximately \( 0.521 \) square units. This area represents the size of the region in the xy-plane where both given inequalities hold true.

Answer 2

The shaded region where inequalities x − 4y2 ≥ 0 and 2 − x − 7|y| ≥ 0 are satisfied is the overlapping area of interest.

Let's break down the inequalities and sketch the regions they define:

1.
`\(x - 4y^2 \geq 0\)`

2.
`\(2 - x - 7|y| \geq 0\)`

To sketch these regions, we'll start with the first inequality:

`\(x - 4y^2 \geq 0\)`

This represents a parabolic region where x is greater than or equal to
`\(4y^2\)`, implying that x is greater or equal to a positive multiple of
`\(y^2\)`. It's an upward opening parabola, centered at the origin.

Now, moving on to the second inequality:

`\(2 - x - 7|y| \geq 0\)`

This represents a combination of two inequalities:
`\(2 - x \geq 7|y|\) and \(-2 + x \leq 7|y|\)`.

Combining these inequalities, we get:

`\(2 - x \geq 7|y|\) and \(x - 2 \leq 7|y|\)`

These represent two lines parallel to the y-axis, splitting the plane into two regions.

Now, let's sketch these regions to find the area of the overlapping region.