Question

You invested $4,000 in an account that has decreased each year. After the first year, the amount in the account was $3,920 and after two years the account had $3,841.60. What is the decay factor?

Answer 1

Decay factor = 0.98

Explanation:

The general equation for exponential decay when dealing with money is given by:

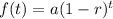`f(t)=a(1-r)^t`, where

• f(t) is the amount in the account after t years,
• a is principal (i.e., the investment),
• (1 - r) is the decay factor,
• and r is the decay rate (as a decimal).

Finding the decay rate:

• Before we can find the decay factor, we need to find the decay rate.

Since the investment was $4000 and the amount in the account after one year was $3920, we can find the decay rate by substituting 4000 for a, 3920 for f(t), and 1 for t:

`3920=4000(1-r)^1\\(3920=4000(1-r))/4000\\(0.98=1-r)-1\\(-0.02=-r)/-1\\0.02=r`

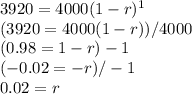
Thus, the decay rate is 0.02.

Determining the decay factor:

Therefore, the decay factor is 0.98 as 1 - 0.02 = 0.98.