Final answer;
The length of
 is
is
 (Option B). This is determined using the Triangle Proportionality Theorem, with the given information about the length of
(Option B). This is determined using the Triangle Proportionality Theorem, with the given information about the length of
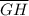 and the parallel lines formed within the triangle.Thus the correct option is:b. 32 units
and the parallel lines formed within the triangle.Thus the correct option is:b. 32 units
Step-by-step explanation:
In the given triangle
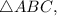 let \( G \) be the point on
let \( G \) be the point on
 and
and
 be the point on
be the point on
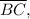 such that
such that
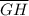 is marked with a length of 16 units.
is marked with a length of 16 units.
To find the length of
 we can use the Triangle Proportionality Theorem, which states that if a line is parallel to one side of a triangle and intersects the other two sides, it divides those sides proportionally.
we can use the Triangle Proportionality Theorem, which states that if a line is parallel to one side of a triangle and intersects the other two sides, it divides those sides proportionally.
Let
 be the point on
be the point on
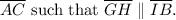 According to the Triangle Proportionality Theorem, we have:
According to the Triangle Proportionality Theorem, we have:
![\[ \frac{\overline{AG}}{\overline{GB}} = \frac{\overline{AI}}{\overline{IC}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/exu0163d6i6axg37brhdszvv3lf9m1ygej.png)
Since
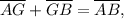 and
and
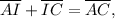 we can set up the proportion:
we can set up the proportion:
![\[ \frac{\overline{AG}}{\overline{AB}} = \frac{\overline{AI}}{\overline{AC}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/v2qlxxxygqkr486u9ua4vthe88chpl3a4n.png)
Given that
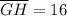 units, we can express
units, we can express
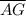 as
as
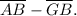 Substituting this into the proportion, we get:
Substituting this into the proportion, we get:
![\[ \frac{\overline{AB} - \overline{GB}}{\overline{AB}} = \frac{\overline{AI}}{\overline{AC}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xk16o0jbamtpxnbvv944vr8g8ik80og0tq.png)
Now, solving for

![\[ \overline{AC} = \frac{\overline{AI} \cdot \overline{AB}}{\overline{AB} - \overline{GB}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/98pzg575amh3matfirfux65jxh7syjf0uv.png)
Finally, substituting the given values, we find:
![\[ \overline{AC} = \frac{16 \cdot \overline{AB}}{\overline{AB} - 16} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5jd17b3p0a1ujhevqklapf5js02zoki3l1.png)
![\[ \overline{AC} = (16 \cdot 48)/(48 - 16) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/86taft7vgdnp5siabikcozde09mj8npomb.png)
![\[ \overline{AC} = (768)/(32) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/msbdnvewxrbsr79jiazeiucx3wuyh3sk8l.png)
![\[ \overline{AC} = 24 \text{ units} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zqt4e0nwmpup50ebsfi68g0x8p35l76j88.png)
Therefore, the length of
 is 24 units, and the correct answer is Option B.
is 24 units, and the correct answer is Option B.