For the multimode fiber, the critical radius of curvature is approximately 0.124 mm, and for the single-mode fiber, it is approximately 0.0099 mm.
To estimate the critical radius of curvature at which large bending losses occur in both cases, we can use the concept of numerical aperture (NA) and the V-number for optical fibers. The critical radius of curvature can be estimated using the formula:
![\[R_c = (d)/(2 \cdot (1 - \cos(\theta_c)))\]](https://img.qammunity.org/2024/formulas/engineering/college/kkc266jdmniwuxw8zqf72hnn23fpr8h7e1.png)
Where:
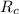 is the critical radius of curvature.
is the critical radius of curvature.
 is the core diameter.
is the core diameter.
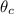 is the maximum angle of incidence at which light can be incident on the core without experiencing significant bending losses.
is the maximum angle of incidence at which light can be incident on the core without experiencing significant bending losses.
Let's calculate the critical radius of curvature for both cases:
Case i: Multimode Fiber
Given parameters:
Core refractive index
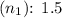
Relative refractive index difference
 : 3% (0.03)
: 3% (0.03)
Operating wavelength
 : 0.82 μm (0.00082 mm)
: 0.82 μm (0.00082 mm)
Core diameter
 : We need to calculate this.
: We need to calculate this.
First, let's calculate the numerical aperture (NA) for this multimode fiber using the formula:
![\[NA = √(n_1^2 - n_2^2)\]](https://img.qammunity.org/2024/formulas/engineering/college/lnuz7ykmduzmjf3ed0t2igko41eudu74jh.png)
Where
 is the refractive index of the cladding. Since it's a multimode fiber, we can assume the cladding refractive index to be close to 1.0 (air). So,
is the refractive index of the cladding. Since it's a multimode fiber, we can assume the cladding refractive index to be close to 1.0 (air). So,
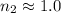 .
.
![\[NA = √(1.5^2 - 1^2) = √(2.25 - 1) = √(1.25) \approx 1.12\]](https://img.qammunity.org/2024/formulas/engineering/college/hj91vs1h74ws6c67rgk1zm7hx3pc9qsyw4.png)
Next, we can calculate the maximum angle of incidence
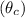 using the formula:
using the formula:
![\[\sin(\theta_c) = (NA)/(n_1)\]](https://img.qammunity.org/2024/formulas/engineering/college/m38qhmi6ltqtbxe3moj6rbcpcsjbxpbb3f.png)
![\[\sin(\theta_c) = (1.12)/(1.5) = 0.7467\]](https://img.qammunity.org/2024/formulas/engineering/college/o5ys0ud0gxw0pzu985zn9g3w9k1vr86jn9.png)
Now, we can find
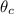 by taking the arcsine:
by taking the arcsine:
![\[\theta_c = \arcsin(0.7467) \approx 49.62^\circ\]](https://img.qammunity.org/2024/formulas/engineering/college/nengehf237jhsy9ltfoquo7n1lqdhss40j.png)
Finally, we can calculate the critical radius of curvature
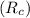 :
:
![\[R_c = (d)/(2 \cdot (1 - \cos(\theta_c)))\]](https://img.qammunity.org/2024/formulas/engineering/college/kkc266jdmniwuxw8zqf72hnn23fpr8h7e1.png)
We know
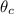 and we can assume a conservative value for
and we can assume a conservative value for
 , say 100 μm (0.1 mm):
, say 100 μm (0.1 mm):
![\[R_c = (0.1)/(2 \cdot (1 - \cos(49.62^\circ)))\]](https://img.qammunity.org/2024/formulas/engineering/college/pt1qdsyz3szedp59tr2et3k4jkxff06rg3.png)
Now, calculate
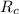 :
:
![\[R_c \approx (0.1)/(2 \cdot (1 - \cos(49.62^\circ))) \approx 0.124 \, \text{mm}\]](https://img.qammunity.org/2024/formulas/engineering/college/o9o6c5sfus1iriauo0v1fpnua8eq95wj0u.png)
Case ii: Single Mode Fiber
Given parameters:
- Core refractive index
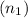 : 1.5
: 1.5 - Relative refractive index difference
 : 0.3% (0.003)
: 0.3% (0.003) - Operating wavelength
 : 1.55 μm (0.00155 mm)
: 1.55 μm (0.00155 mm) - Core diameter
 : 8 μm (0.008 mm)
: 8 μm (0.008 mm)
First, let's calculate the numerical aperture (NA) for this single-mode fiber:
![\[NA = √(n_1^2 - n_2^2)\]](https://img.qammunity.org/2024/formulas/engineering/college/lnuz7ykmduzmjf3ed0t2igko41eudu74jh.png)
As before, we can assume
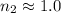 :
:
![\[NA = √(1.5^2 - 1^2) = √(2.25 - 1) = √(1.25) \approx 1.12\]](https://img.qammunity.org/2024/formulas/engineering/college/hj91vs1h74ws6c67rgk1zm7hx3pc9qsyw4.png)
Next, calculate the maximum angle of incidence
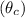 :
:
![\[\sin(\theta_c) = (NA)/(n_1)\]](https://img.qammunity.org/2024/formulas/engineering/college/m38qhmi6ltqtbxe3moj6rbcpcsjbxpbb3f.png)
![\[\sin(\theta_c) = (1.12)/(1.5) = 0.7467\]](https://img.qammunity.org/2024/formulas/engineering/college/o5ys0ud0gxw0pzu985zn9g3w9k1vr86jn9.png)
Now, find
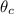 by taking the arcsine:
by taking the arcsine:
![\[\theta_c = \arcsin(0.7467) \approx 49.62^\circ\]](https://img.qammunity.org/2024/formulas/engineering/college/nengehf237jhsy9ltfoquo7n1lqdhss40j.png)
Finally, calculate the critical radius of curvature
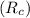 :
:
![\[R_c = (d)/(2 \cdot (1 - \cos(\theta_c)))\]](https://img.qammunity.org/2024/formulas/engineering/college/kkc266jdmniwuxw8zqf72hnn23fpr8h7e1.png)
We know
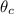 and
and
 :
:
![\[R_c = (0.008)/(2 \cdot (1 - \cos(49.62^\circ)))\]](https://img.qammunity.org/2024/formulas/engineering/college/x20sdgja9bkdcbl0q4e0r1wmwk1xdose6b.png)
Calculate
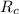 :
:
![\[R_c \approx (0.008)/(2 \cdot (1 - \cos(49.62^\circ))) \approx 0.0099 \, \text{mm}\]](https://img.qammunity.org/2024/formulas/engineering/college/ko0s7oqf5yc4untjyglg9vwxfowf2vr33h.png)
So, in both cases, the critical radius of curvature at which large bending losses occur is approximately 0.124 mm for the multimode fiber and 0.0099 mm for the single-mode fiber.
The complete question is here:
Two step index fibers exhibit the following parameters.
i) A multimode fiber with a core refractive index of 1.5 , a relative refractive index difference of 3% and an operating wavelength of 0.82μm.
ii) An 8μm core diameter single mode fiber with a core refractive index of 1.5 , relative refractive index difference of 0.3% and an operating wavelength of 1.55μm. istimate the critical radius of curvature at which large bending losses occur in both the cases.