Question

Adult tickets to a basketball game cost $5. Student tickets cost $1. A total of $3,047

was collected on the sale of 1,291 tickets. How many of each type of ticket were sold?
The basketball game sold
adult tickets and
student tickets.

Answer 1

The basketball game sold 439 adult tickets and 858 student tickets.

Explanation:

A system of linear equations is a set of two or more equations of the first degree, in which two or more unknowns are related.

Solving a system of equations consists of finding the value of each unknown so that all the equations of the system are satisfied. That is, in the systems of equations, one must look for the values ​​of the unknowns, with which when replacing, they must give the solution proposed in both equations.

Adult tickets to a basketball game cost $5. Student tickets cost $1. A total of $3,047 was collected on the sale of 1,291 tickets.

With "x" the number of adult tickets sold and "y" the number of student tickets sold, you have the following system of equations:

`\left \{ {{x+y=1291} \atop {5*x+1*y=3047}} \right.`

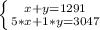
Through the substitution method, you must solve for one of the unknowns in one of the equations and substitute its value in the following one: in this case you solve for the variable y from the first equation:

y=1291 -x

and you replace in the second equation:

5*x + 1291 - x= 3047

Solving, you get:

5*x-x= 3047 - 1291

4*x= 1756

x= 1756÷4

x=439

Replacing this value in the expresion y=1291 -x you get:

y=1291 -439

y= 858

The basketball game sold 439 adult tickets and 858 student tickets.