Question

Rewrite the logarithm as a ratio of common logarithms and natural logarithms.

log2.8(x)
(a) common logarithms
X
(b) natural logarithms

Answer 1

`\textsf{a)} \quad (\log(x))/(\log(2.8))`

`\textsf{b)} \quad (\ln(x))/(\ln(2.8))`

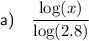
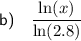
Explanation:

Part (a)

The common logarithm is the logarithm with base 10. It is often written as log without a specified base:

`\log_(10)(x)=\log(x)`

To rewrite
`log_(2.8)(x)` as a ratio of common logarithms, we can use the change of base formula.

The change of base formula is:

`\large\boxed{\log_ba=(\log_na)/(\log_nb)}`

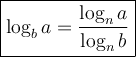
where n is the new base.

In our case:

• a = x
• b = 2.8
• n = 10

Substituting the values into the change of base formula gives:

`\log_(2.8)(x)=(\log_(10)(x))/(\log_(10)(2.8))`

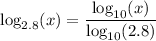
As the common logarithm is often written as log without a specified base, this can also be written as:

`\log_(2.8)(x)=(\log(x))/(\log(2.8))`

`\hrulefill`

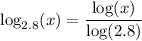
Part (b)

The natural logarithm is the logarithm with base e, where e is the Euler's constant approximately equal to 2.7182818 (7 d.p.). It is usually written as "ln":

`\log_e(x)=\ln (x)`

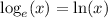
To rewrite
`log_(2.8)(x)` as a ratio of natural logarithms, we can use the change of base formula.

The change of base formula is:

`\large\boxed{\log_ba=(\log_na)/(\log_nb)}`

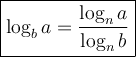
where n is the new base.

In our case:

• a = x
• b = 2.8
• n = e

Substituting the values into the change of base formula gives:

`\log_(2.8)(x)=(\log_(e)(x))/(\log_(e)(2.8))`

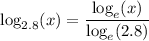
As the natural logarithm is often written as "ln", this can also be written as:

`\log_(2.8)(x)=(\ln(x))/(\ln(2.8))`