Answer:
Isosceles
Explanation:
Use distance formula:
d =
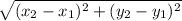
Find distance between each point, there should be 3 lengths given after we find it. Once we find the length of each side, we will use the Pythagorean theorem to check and see if it is a right angle.
Let's first find out what each of these terms mean:
Right triangle: A triangle with one angle measuring 90 degrees.
Scalene triangle: A triangle with all sides not equal to each other at all.
Isosceles triangle: A triangle that has two sides of equal length.
Now let's find the distance between all sets of pairs of coordinates when (0, -2) to (-5, 4) form a length and (-5, 4) to (5, 4) form another length, and finally (5, 4) to (0, -2) form the last length.
We could also verify this with a graph in the end.
d =
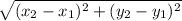
(0, -2) to (-5, 4) are our first coordinate set to solve, we'll call (0, -2) the first pair and (-5, 4) the second:
Substitute:
d =
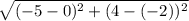
Evaluate parenthesis first:
d =
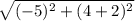
d =
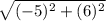
Solve exponents:
d =
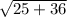
d =
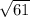
Let's keep
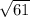 under a radical to compare lengths in the end.
under a radical to compare lengths in the end.
Now to find our second length, we'll call (-5, 4) our first pair and (5, 4) our second:
d =
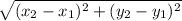
d =
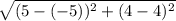
d =
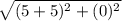
d =
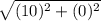
d =

d =
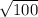
Which square roots perfectly into:
d = 10
Finally, the third length,
we'll call (5, 4) our first pair and (0, -2) our second:
d =
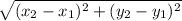
d =

d =

d =
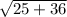
d =
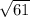
Now let's compare all the lengths together:
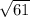 ,
,
 ,
,
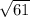
We can see that the first and third lengths are the same(
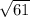 and
and
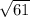 ). And judging from all the classifications of a triangle, this seems to fit the category of an isosceles triangle!
). And judging from all the classifications of a triangle, this seems to fit the category of an isosceles triangle!
Two lengths of a triangle that are congruent(the same) are an isosceles triangle.
Therefore this triangle is isosceles.