Answer:
36.4, but to be more precise, 36.359
Explanation:
Let's use the distance formula.
Distance formula:
d =
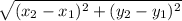
Where (x1, y1) represents a pair of coordinates and (x2, y2) represent the second set of coordinates.
Now, to find the lengths of all three sides of the triangle, we must calculate the distance between each and every point starting from (8, 0) to (-3, 9) and (-3, 9) to (-7, 10), then lastly from (-7, 10) to (8, 0).
Once we plug each of these sets of pairs of coordinates in the distance formula, we'll add all the lengths up to get the perimeter (since that is what perimeter is, the sum of all the edges/boundaries of a figure).
Let's solve the distance between (8, 0) and (-3, 9) now,
let's call (8, 0) the first pair and (-3, 9) the second:
d =
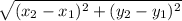
Substitute:
d =
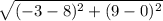
Solve in parenthesis first:
d =
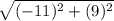
Then solve exponents:
d =
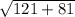
Add:
d =

It cannot be simplified any further so let's just evaluate and round:
d ≈ 14.213
Now, we've found the distance between the first set of coordinates. Let's find the second,
(-3, 9) is the first coordinate pair and (-7, 10) is the second coordinate pair:
d =
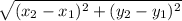
d =
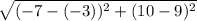
d =
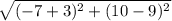
d =

d =
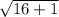
d =

Cannot be simplified further so just evaluate and round:
d ≈ 4.123
Now let's find the third length (we're so close!),
(-7, 10) is our first pair of coordinates and (8, 0) is our second:
d =
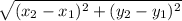
d =

d =

d =
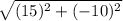
d =

d =
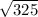
Can be simplified, but at this point just evaluate since we evaluated our other distances, evaluate and round:
d ≈ 18.023
Now that we've found all our distances, let's add them up:
14.213 + 4.123 + 18.023
≈ 36.359 is the perimeter of this triangle.
If you wanted to round to the nearest tenth:
≈ 36.4