Question

What is the equation of the parabola and how can I find it?

Answer 1

I can't see the image...

Answer 2

`y=x^2-x-2`

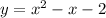
Explanation:

The equation of a graphed vertical parabola (opening upward or downward) is a quadratic equation.

The factored form of a quadratic equation is:

`\large\boxed{y=a(x-r_1)(x-r_2)}`

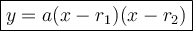
where:

• a is the leading coefficient.
• r₁ and r₂ are the roots (x-intercepts).

The graphed parabola crosses the x-axis at (-1, 0) and (2, 0), so its x-intercepts (roots) are x = -1 and x = 2. Therefore:

• r₁ = -1
• r₂ = 2

Substitute the roots into the equation:

`y=a(x-(-1))(x-2)`

`y=a(x+1)(x-2)`

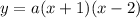
The parabola passes through the point (1, -2).

To find the leading coefficient (a), we can substitute point (1, -2) into the equation, and solve for a:

`-2=a(1+1)(1-2)`

`-2=a(2)(-1)`

`-2=-2a`

`a=1`

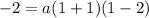
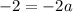
Therefore, the factored equation of the parabola is:

`y=1(x+1)(x-2)`

`y=(x+1)(x-2)`

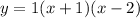
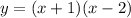
To write this in standard form, expand the brackets:

`y=x^2-2x+x-2`

`y=x^2-x-2`

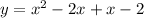
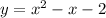
Therefore, the equation of the parabola is:

`\large\boxed{\boxed{y=x^2-x-2}}`