Question

C(x) = 17000+500x-1.6x²+0.004x³ is the cost function and p(x)=1700-7x is the demand function, find the production level will maximum profit. (Hint: If the profit is maximized, then the marginal revenue equals the marginal cost).

Answer 1

To find the production level that maximizes profit, we need to set the marginal revenue equal to the marginal cost.

Step-by-step explanation:

To find the production level that will result in maximum profit, we need to determine the output level at which the marginal revenue equals the marginal cost. The profit is maximized when the marginal revenue equals the marginal cost. The marginal revenue can be found by taking the derivative of the demand function, p(x), which is -7. The marginal cost can be found by taking the derivative of the cost function, C(x), which is 500 - 3.2x + 0.012x^2. Setting the marginal revenue equal to the marginal cost and solving for x gives us the production level that will result in maximum profit.

Answer 2

The production level that maximizes profit is approximately 125.

To find the production level that maximizes profit, we need to set the marginal revenue equal to the marginal cost. The marginal revenue (MR) is the derivative of the revenue function, and the marginal cost (MC) is the derivative of the cost function. The profit function (P) is given by subtracting the cost function from the revenue function:

`P(x)=R(x)-C(x)`

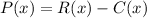
First, let's calculate the revenue function R(x) using the demand function p(x):

`R(x)=p(x) \cdot x=(1700-7 x) \cdot x`

Now, calculate the profit function P(x):

`\begin{aligned}& P(x)=R(x)-C(x) \\& P(x)=(1700-7 x) \cdot x-\left(17000+500 x-1.6 x^2+0.004 x^3\right)\end{aligned}`

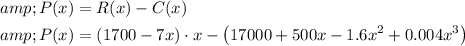
Simplify the Profit Function:

`\begin{aligned}& P(x)=1700 x-7 x^2-17000-500 x+1.6 x^2-0.004 x^3 \\& P(x)=-0.004 x^3+1.6 x^2-507 x-17000\end{aligned}`

The Derivative of the Profit Function P'(x):

`P^(\prime)(x)=-0.012 x^2+3.2 x-507`

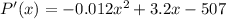
Now, let's set P'(x) equal to zero and solve for x:

`-0.012 x^2+3.2 x-507=0`

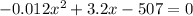
Using the quadratic formula:

`x=(-b \pm √(b^2-4 a c))/(2 a)`

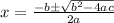
In this case, a=−0.012, b=3.2, and c=−507.

`\begin{aligned}& x=(-3.2 \pm √((3.2)^2-4(-0.012)(-507)))/(2(-0.012)) \\& x \approx 125\end{aligned}`

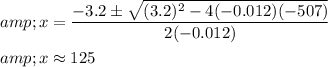
The correct value for x that maximizes profit is approximately 125.