Question

⚠️GIVING 50 POINTS TO THE 1ST PERSON WHO ANSWERS⚠️

A ​40-inch board is to be cut into three pieces so that the second piece is 4 times as long as the first piece and the third piece is 5 times as long as the first piece. If x represents the length of the first​ piece, find the lengths of all three pieces.

Answer 1

Let's set up equations to solve this problem. You have three pieces, and you know their relative lengths:

1. The first piece is x inches long.
2. The second piece is 4 times as long as the first, so its length is 4x inches.
3. The third piece is 5 times as long as the first, so its length is 5x inches.

Now, you're given that the total length of the board is 40 inches. So, the sum of the lengths of these three pieces should be equal to 40 inches:

x + 4x + 5x = 40

Now, combine like terms:

10x = 40

To find the value of x, divide both sides by 10:

x = 40 / 10
x = 4

Now that you know the length of the first piece (x = 4 inches), you can find the lengths of the other two pieces:

1. First piece: x = 4 inches
2. Second piece: 4x = 4 * 4 = 16 inches
3. Third piece: 5x = 5 * 4 = 20 inches

So, the three pieces are 4 inches, 16 inches, and 20 inches long, respectively.

Answer 2

First piece: 4 inches

Second piece: 16 inches

Third piece: 20 inches

Explanation:

Let's say the length of the first piece is x inches.

The second piece is 4 times as long as the first piece, so its length is 4x inches.

The third piece is 5 times as long as the first piece, so its length is 5x inches.

Together, the three pieces must have a total length of 40 inches.

So we have the equation:

`\sf x + 4x + 5x = 40`

Combining like terms, we get:

10x = 40

Dividing both sides by 10, we get:

`\sf x =(40)/(10)`

`\sf x = 4`

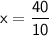
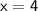
Therefore, the lengths of the three pieces are:

First piece: x = 4 inches

Second piece: 4x = 4 × 4 = 16 inches

Third piece: 5x = 5 × 4 = 20 inches