Question

Santiago is going to invest in an account paying an interest rate of 1.5% compounded quarterly. how much would santiago need to invest, to the nearest dollar, for the value of the account to reach $320 in 14 years?

Answer 1

Santiago would need to invest approximately $260 to the nearest dollar for the value of the account to reach $320 in 14 years when the interest rate is 1.5% compounded quarterly.

To find out how much Santiago needs to invest in an account to reach a value of $320 in 14 years with an interest rate of 1.5% compounded quarterly, you can use the compound interest formula:

`\[A = P \left(1 + (r)/(n)\right)^(nt)\]`

Where:

-
`\(A\)` is the future value of the investment ($320 in this case).

-
`\(P\)` is the initial principal (the amount Santiago needs to invest).

-
`\(r\)` is the annual interest rate (1.5% or 0.015 as a decimal).

-
`\(n\)` is the number of times the interest is mixed per year (quarterly, so
`\(n = 4\)`).

-
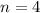`\(t\)` is the number of years (14 years in this case).

We need to solve for
`\(P\)`, so let's rearrange the formula:

`\[P = (A)/(\left(1 + (r)/(n)\right)^(nt))\]`

Now, plug in the values:

`\[P = (320)/(\left(1 + (0.015)/(4)\right)^(4 * 14))\]`

Calculate the exponent:

`\[P = (320)/(\left(1 + 0.00375\right)^(56))\]`

Now, calculate the expression inside the parentheses:

`\[P = (320)/((1.00375)^(56))\]`

Calculate the value inside the parentheses:

`\[P = (320)/(1.22804768215)\]`

Now, divide to find the value of
`\(P\)`:

`\[P \approx (320)/(1.22804768215) \approx 260.19\]`

So, Santiago would need to invest approximately $260 (rounded to the nearest dollar) for the value of the account to reach $320 in 14 years with an interest rate of 1.5% compounded quarterly.

Answer 2

The principal investment required to get a total amount of $320 from compound interest at a rate of 1.5% per year compounded 4 times per year over 14 years is $260.

The formula for compound interest is expressed as:

`A = P( 1 + (r)/(n))^(nt)`

Where A is the accrued amount, P is the principal, r is the interest rate and t is time.

Given that:

Accrued amount A = $320

Interest rate r = 1.5% = 1.5/100 = 0.015

Compounded quarterly n = 4

Time t = 14 years

Principal P =?

Plug the given values into the above formula and solve for the principal:

`A = P( 1 + (r)/(n))^(nt)\\\\P = (A)/(( 1 + (r)/(n))^(nt) ) \\\\P = (320)/(( 1 + (0.015)/(4))^(4*14) ) \\\\P = (320)/(( 1 + 0.00375)^(4*14) ) \\\\P = (320)/(( 1.00375)^(4*14) ) \\\\P = \$260`

Therefore, Santiago needs to invest approximately $260.