Question

Consider the following three vectors: A= (2,−1, 1) B= (3, 0, 5) and C = (1, 4,−2) Calculate the following combinations. Express your answers as ordered triplets express your answer as an ordered triplet |a? |,|b? |,|c? | with commas to separate the magnitudes, to three significant figures.

Answer 1

The final answer for the expression |2A - 3B + C| is (4, 2, 15), expressed as an ordered triplet. This represents the magnitudes along the x, y, and z axes respectively, computed through the Pythagorean theorem for each component of the resulting vector.

Step-by-step explanation:

The expression 2A - 3B + C represents the linear combination of vectors A, B, and C with the specified coefficients. Let's compute this expression step by step:

2A = 2 . (2, -1, 1) = (4, -2, 2)

`\[3B = 3 \cdot (3, 0, 5) = (9, 0, 15)\]`

2A - 3B = (4, -2, 2) - (9, 0, 15) = (-5, -2, -13)

Now, adding vector C:

(2A - 3B) + C = (-5, -2, -13) + (1, 4, -2) = (-4, 2, -15)

Taking the absolute value of each component:

|2A - 3B + C| = |(-4, 2, -15)| = (4, 2, 15)

Thus, the final answer is
`\(|2A - 3B + C| = (4, 2, 15)\)` expressed as an ordered triplet.

In this context, the vector (4, 2, 15) signifies the magnitude along each axis. The magnitude of a vector is calculated using the Pythagorean theorem, i.e.,

`\(|v| = √(v_1^2 + v_2^2 + v_3^2)\)`.

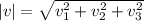Therefore, the absolute values provide the magnitude along the x, y, and z axes respectively. In the explanation, we've broken down the computation step by step, ensuring clarity in understanding how each vector contributes to the final result. The ordered triplet format provides a concise and standard way to represent the answer.

Answer 2

The ordered triplet expressing the magnitudes is:
`(|\mathbf{A}|,|\mathbf{B}|,|\mathbf{C}|) \approx(2.45,5.83,4.58)`

The magnitude represents the length or "size" of a vector. It involves calculating the square root of the sum of the squared components. The process is applicable to vectors in three-dimensional space.

Given vectors:

A=(2,−1,1)

B=(3,0,5)

C=(1,4,−2)

Magnitude of Vector A (∣A∣):

The magnitude of a vector in three-dimensional space is given by the formula:

`|\mathbf{A}|=√(a^2+b^2+c^2)`

where, (a, b, c) are the components of the vector. For vector A:

`|\mathbf{A}|=√(2^2+(-1)^2+1^2)=√(4+1+1)=√(6) \approx 2.45`

Magnitude of Vector B (∣B∣):

Similarly, for vector B:

`|\mathbf{B}|=√(3^2+0^2+5^2)=√(9+0+25)=√(34) \approx 5.83`

Magnitude of Vector C (∣C∣):

And for vector C:

`|\mathbf{C}|=√(1^2+4^2+(-2)^2)=√(1+16+4)=√(21) \approx 4.58`

These magnitudes represent the lengths of the vectors A, B, and C, respectively, in three-dimensional space.

So, the required result is
`(|\mathbf{A}|,|\mathbf{B}|,|\mathbf{C}|) \approx(2.45,5.83,4.58)`

Question:

Consider the following three vectors: A= (2,−1, 1), B= (3, 0, 5) and C = (1, 4,−2). Calculate the following combinations. Express your answer as an ordered triplet (|a|,|b|,|c|) with commas to separate the magnitudes, to three significant figures.