Question

Find the distance between the given parallel planes. 2z = 6y − 4x, 3z = 2 − 6x + 9y

Answer 1

The distance between the two parallel planes is
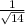`\((1)/(√(14))\)`units.

The given parallel planes are represented by the equations:

1. 2z = 6y - 4x

2. 3z = 2 - 6x + 9y

To find the distance between these parallel planes, we can use the formula:

`\[ \text{Distance} = (\left|D_2 - D_1\right|)/(√(A^2 + B^2 + C^2)) \]`

where the equations of the planes are in the form Ax + By + Cz = D.

Let's rewrite the given equations in the form Ax + By + Cz = D:

1.
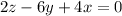
`\(2z - 6y + 4x = 0\)`

2.
`\(3z + 6x - 9y - 2 = 0\)`

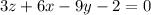
Now, we can use the coefficients \(A\), \(B\), \(C\), and \(D\) in the formula.

For Plane 1:

`\[ A_1 = 4, \quad B_1 = -6, \quad C_1 = 2, \quad D_1 = 0 \]`

For Plane 2:

`\[ A_2 = 6, \quad B_2 = -9, \quad C_2 = 3, \quad D_2 = 2 \]`

Now, plug these values into the formula:

`\text{Distance} = (\left|2 - 0\right|)/(√(4^2 + (-6)^2 + 2^2)) \]\\\text{Distance} = (2)/(√(16 + 36 + 4)) \]\\\text{Distance} = (2)/(√(56)) \]\\ \text{Distance} = (2)/(2√(14)) \]\\ \text{Distance} = (1)/(√(14)) \]`

So, the distance between the given parallel planes is
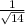`\((1)/(√(14))\)`.