Question

Show that the equation represents a sphere, and find its center and radius. 17. x² + y² + z² - 2x - 4y + 8z 15

Answer 1

I'll assume the equation given to you is

`x^2+y^2+z^2-2x-4y+8z = 15`

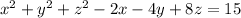
Please let me know if this assumption is incorrect. If so, then I'll make a correction.

-----------------

We must complete the square for each variable x, y, and z.

`x^2+y^2+z^2-2x-4y+8z = 15\\\\(x^2-2x)+(y^2-4y)+(z^2+8z) = 15\\\\(x^2-2x+0)+(y^2-4y+0)+(z^2+8z+0) = 15\\\\(x^2-2x+1-1)+(y^2-4y+4-4)+(z^2+8z+16-16) = 15\\\\((x-1)^2-1)+((y-2)^2-4)+((z+4)^2-16) = 15\\\\(x-1)^2+(y-2)^2+(z+4)^2+(-1-4-16) = 15\\\\(x-1)^2+(y-2)^2+(z+4)^2-21 = 15\\\\(x-1)^2+(y-2)^2+(z+4)^2 = 15+21\\\\(x-1)^2+(y-2)^2+(z+4)^2 = 36\\\\(x-1)^2+(y-2)^2+(z-(-4))^2 = 6^2\\\\`

-----------------

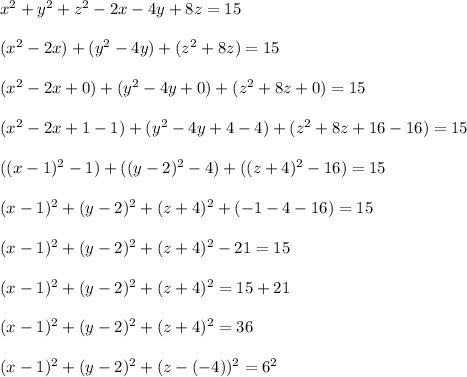
The template
`(x-a)^2+(y-b)^2+(z-c)^2 = r^2` represents a sphere centered at (a,b,c) and has radius r.

The final equation in the previous section matches the template perfectly, which confirms we have a sphere.

We see that:

• a = 1
• b = 2
• c = -4
• r = 6

Therefore, the sphere
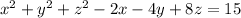`x^2+y^2+z^2-2x-4y+8z = 15` is centered at (x,y,z) = (1,2,-4) and has radius r = 6.