Question

If you deposit $5000 into an account paying 6% annual interest, how long until there is $8000 in the account?

Answer 1

To find out how long it will take for $5000 to grow to $8000 at an annual interest rate of 6%, we need to use the formula for compound interest. Plugging in the values, we find that it will take approximately 3.82 years for the account to grow to $8000.

Step-by-step explanation:

To find out how long it will take for $5000 to grow to $8000 at an annual interest rate of 6%, we need to use the formula for compound interest:

`A = P(1 + r/n)^(nt)`

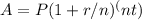
Where:

• A is the future value of the investment ($8000 in this case)
• P is the principal amount ($5000)
• r is the annual interest rate (6% or 0.06)
• n is the number of times the interest is compounded per year (typically 1)
• t is the number of years

Plugging in the values, we get:

`8000 = 5000(1 + 0.06/1)^(1t)`

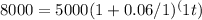
Now we can solve for t. Rearranging the equation:

`1.6 = (1.06)^t`

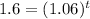
Using logarithms, we find that t is approximately 3.82 years. Therefore, it will take approximately 3.82 years for the account to grow to $8000.

Answer 2

To have $8000 in an account that pays 6% annual interest when you deposit $5000, it would take approximately 4.25 years.

Step-by-step explanation:

To find out how long it will take for $5000 to grow to $8000 with an annual interest rate of 6%, we can use the formula for compound interest:

A = P(1 + r/n)^(nt)

Where:

• A is the final amount (in this case, $8000)
• P is the principal amount (in this case, $5000)
• r is the annual interest rate (in this case, 6% or 0.06)
• n is the number of times interest is compounded per year (since it's not specified, we'll assume it's compounded annually)
• t is the number of years (which we need to find)

Substituting the given values into the formula:

`8000 = 5000(1 + 0.06/1)^(1*t)`

`8000/5000 = (1.06)^t1.6 = (1.06)^t`,

we take the natural logarithm of both sides:

`ln(1.6) = ln((1.06)^t)t*ln(1.06) = ln(1.6)t = ln(1.6)/ln(1.06)`