Question

If x_(1),x_(2) are the solutions of the equation 4^(3x^(2))=(1)/(16^(3x+1)) compute the value of |x_(1)-x_(2)|. Select all that apply

Answer 1

Given that x_(1),x_(2) are the solutions of the equation, the value of |x₁ - x₂| is 2/3√(15).

How to find the value of |x₁ - x₂|

To find the value of |x₁ - x₂|, find the solutions x₁ and x₂ of the equation
`4^(3x^2) = (1)/(16^(3x+1)).`

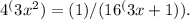
simplify the equation step by step:

`4^(3x^2) = (1)/(16^(3x+1))`

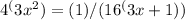
Rewriting 4 and 16 as powers of 2:

`(2^2)^(3x^2) = (1)/((2^4)^(3x+1))`

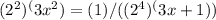
Applying the power of a power rule:

`2^(2 * 3x^2) = (1)/(2^(4 * (3x+1)))`

`2^(6x^2) = (1)/(2^(12x + 4))`

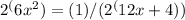
Now equate the bases:

`6x^2 = 12x + 4`

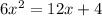
Rearranging the equation to form a quadratic equation:

`6x^2 - 12x - 4 = 0`

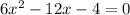
Divide the equation by 2:

3x^2 - 6x - 2 = 0

Solve this quadratic equation using the quadratic formula:

x = (-b ± √(
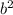`b^2` - 4ac))/(2a),

where a = 3, b = -6, and c = -2.

Plug in the values:

x = (-(-6) ± √(
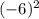`(-6)^2` - 4 * 3 * (-2)))/(2 * 3)

x = (6 ± √(36 + 24))/(6)

x = (6 ± √(60))/(6)

x = (6 ± √(4 * 15))/(6)

x = (6 ± 2√(15))/(6)

x = 1 ± (1/3)√(15)

Therefore, the solutions to the equation are x₁ = 1 + (1/3)√(15) and x₂ = 1 - (1/3)√(15).

To find |x₁ - x₂|, substitute the values:

|x₁ - x₂| = |(1 + (1/3)√(15)) - (1 - (1/3)√(15))|

|x₁ - x₂| = |2/3√(15)|

|x₁ - x₂| = 2/3√(15)

Therefore, the value of |x₁ - x₂| is 2/3√(15).