At (t ≈ 3.47) years, the revenue peaks. At this time, the revenue is approximately \$47.3 million, derived from (R(3.47) ≈ 47332.5) million dollars.
Given:
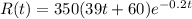 million dollars
million dollars
(a) To determine when the revenue peaks, find
 when
when
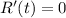 , where
, where
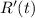 is the derivative of
is the derivative of
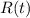 .
.
The derivative of
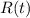 with respect to
with respect to
 can be found using the product rule and chain rule:
can be found using the product rule and chain rule:
Given
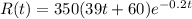 ,
,
![\[ R'(t) = 350 \cdot (39)e^(-0.2t) + 350(39t + 60) \cdot (-0.2)e^(-0.2t) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rt1sxs38gv8zoc11fth7hfh9p6n99k1g3y.png)
Setting
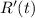 to zero to find the critical points:
to zero to find the critical points:
![\[ 350 \cdot (39)e^(-0.2t) + 350(39t + 60) \cdot (-0.2)e^(-0.2t) = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rjagvxp5gdut0zwvbwed0sx3rh9lmni90z.png)
Factor out
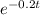 :
:
![\[ e^(-0.2t)(350 \cdot 39 - 350(39t + 60) \cdot 0.2) = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/plp0wqa0w26lt1amuld2er5djovkiegm27.png)
Solve for
 :
:
![\[ 350 \cdot 39 - 350(39t + 60) \cdot 0.2 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/l0g3tx3jyligq4hojc3z34bw287s0rth3g.png)
![\[ 13650 - 70(39t + 60) = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/osfrrtqntux8v82aui12e1xq882q7ib2r5.png)
![\[ 13650 - 2730t - 4200 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kxq7ysjlj22nubtzn800uj7a014yr7f7ng.png)
![\[ 9450 - 2730t = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/81h19l5u68rzm27wdgwmba7ur77csn6gi7.png)
![\[ 2730t = 9450 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8y9yzezy5502zibv8ummnzzhu98xt1xs15.png)
![\[ t = (9450)/(2730) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ox51tvos3wnbq5srvt0r41gtg2l9yhlplt.png)
t ≈ 3.47 { years (to the nearest 0.1 year)}
(b) To find the revenue at \(t ≈ 3.47\) years, substitute this value into \(R(t)\):
![\[ R(3.47) = 350(39 \cdot 3.47 + 60)e^(-0.2 \cdot 3.47) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6glukcn81rd0osskaz2u8bjmo048ops6k3.png)
![\[ R(3.47) = 350(135.33)e^(-0.694) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qkif17282oszuoqzbxq9vze9xayvxleocq.png)
R(3.47) ≈ 47332.5 { million dollars (to the nearest million)}
Therefore, at \(t ≈ 3.47\) years, the revenue is approximately \$47.3 million.
the completed question:
Model the annual revenue as \(R(t) = 350(39t+60)e^{-0.2t}\) million dollars.
(a) Calculate, to the nearest 0.1 year, when the revenue was projected to peak. Provide your answer in terms of \(t\).
(b) Calculate the revenue, rounded to the nearest \$1 million, at that time. Submit your answer in millions of dollars.