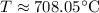Question

Water gas, a mixture of H₂ and CO₂ is a fuel made by reacting steam with red-hot coke (a by product of coal distillation): H₂O (g) + C(s) ⇆ CO(g) + H₂ (g) Using a table of thermodynamic data, estimate the temperature at which the reaction begins to favor the formation of products. ____°C

Answer 1

The estimated temperature at which the reaction begins to favor the formation of products is approximately 708.05°C.

To estimate the temperature at which the reaction begins to favor the formation of products, we can use the concept of Gibbs free energy (ΔG) and the relationship:

`\Delta G=\Delta H-T \cdot \Delta S`

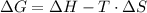
At equilibrium, ΔG=0. Therefore, we can rearrange the equation to solve for the temperature (T):

`T=(\Delta H)/(\Delta S)`

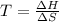
Where:

ΔH is the enthalpy change of the reaction.

ΔS is the entropy change of the reaction.

We need to refer to thermodynamic data to obtain ΔH and ΔS for the reaction:

`\mathrm{H}_2 \mathrm{O}(g)+\mathrm{C}(\mathrm{s}) \rightleftharpoons \mathrm{CO}(\mathrm{g})+\mathrm{H}_2(g)`

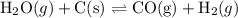
Using the standard enthalpies of formation
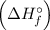`\left(\Delta H_f^(\circ)\right)` and standard entropies
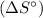`\left(\Delta S^(\circ)\right)` for each species, we can calculate ΔH and ΔS.

For standard thermodynamic data, we have:

`\begin{aligned}& \Delta H_f^(\circ)\left(\mathrm{H}_2 O\right)=-241.82 \mathrm{~kJ} / \mathrm{mol} \\& \Delta H_f^(\circ)(\mathrm{C})=0 \mathrm{~kJ} / \mathrm{mol} \\& \Delta H_f^(\circ)(\mathrm{CO})=-110.53 \mathrm{~kJ} / \mathrm{mol} \\& \Delta H_f^(\circ)\left(\mathrm{H}_2\right)=0 \mathrm{~kJ} / \mathrm{mol}\end{aligned}`

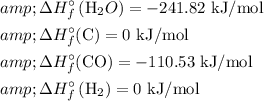
Let's calculate ΔH using these values:

`\begin{aligned}& \Delta H=\sum \Delta H_f^(\circ)(\text { products })-\sum \Delta H_f^(\circ)(\text { reactants }) \\& \Delta H=[-110.53+0]-[(-241.82+0)] \mathrm{kJ} / \mathrm{mol} \\& \Delta H \approx 131.29 \mathrm{~kJ} / \mathrm{mol}\end{aligned}`

For the entropy change ΔS, we can use standard entropy values:

`\begin{aligned}& \Delta S^(\circ)\left(\mathrm{H}_2 O\right)=188.72 \mathrm{~J} / \mathrm{mol} \mathrm{K} \\& \Delta S^(\circ)(\mathrm{C})=5.74 \mathrm{~J} / \mathrm{mol} \mathrm{K} \\& \Delta S^(\circ)(\mathrm{CO})=197.67 \mathrm{~J} / \mathrm{mol} \mathrm{K} \\& \Delta S^(\circ)\left(\mathrm{H}_2\right)=130.68 \mathrm{~J} / \mathrm{mol} \mathrm{K}\end{aligned}`

`\begin{aligned}& \Delta S=\sum \Delta S^(\circ)(\text { products })-\sum \Delta S^(\circ)(\text { reactants }) \\& \Delta S=[197.67+130.68]-[188.72+5.74] \mathrm{J} / \mathrm{mol} \mathrm{K} \\& \Delta S \approx 133.89 \mathrm{~J} / \mathrm{mol} \mathrm{K}\end{aligned}`

Now, substitute these values into the temperature equation:

`\begin{aligned}& T=(\Delta H)/(\Delta S) \\& T \approx \frac{131.29 \mathrm{~kJ} / \mathrm{mol}}{133.89 \mathrm{~J} / \mathrm{mol} \mathrm{K}} \\& T \approx 981.20 \mathrm{~K}\end{aligned}`

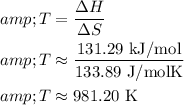
Convert to Celsius:

`T \approx 708.05^(\circ) \mathrm{C}`