Question

Suppose that a candy bar advertises on its wrapper that its weight is 54.5 grams. The actual weights vary a bit from candy bar to candy bar. Let’s suppose that the actual weights follow a normal distribution with mean μμ= 55.0 grams and standard deviation σσ= 0.3 grams. Determine the value of the mean that would achieve the goal that only 1% of candy bars weigh less than advertised.Which of the following best describes the downside to the manufacturer of making the change in Q3.3?

Answer 1

The value of the mean that would achieve the goal that only 1% of candy bars weigh less than advertised is approximately 54.49 grams.

Step-by-step explanation:

To find the mean weight that ensures only 1% of candy bars weigh less than advertised, we can use the Z-score formula. The Z-score is calculated as:

`\[ Z = \frac{{X - \mu}}{{\sigma}} \]`

Where:

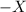`- \( X \)` is the value we want to find (mean in this case),

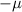`- \( \mu \)` is the given mean (55.0 grams),

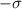`- \( \sigma \)` is the given standard deviation (0.3 grams).

For a 1% probability, the Z-score is approximately -2.33 (as the normal distribution is symmetric). Rearranging the formula to solve for X , we get:

`\[ X = Z \cdot \sigma + \mu \]`

Substituting the values, we find:

`\[ X = (-2.33) \cdot 0.3 + 55.0 \]`

Calculating this gives us the mean X as approximately 54.49 grams. This means that setting the mean weight to 54.49 grams would ensure that only 1% of candy bars weigh less than advertised.

The downside to the manufacturer of making this change is potential customer dissatisfaction and legal implications. If customers consistently receive candy bars that weigh less than advertised, it can harm the brand's reputation and lead to decreased customer trust. Additionally, there may be legal consequences if the product consistently falls below the advertised weight, as it could be considered false advertising. Maintaining the advertised weight is crucial for customer satisfaction and legal compliance.