Question

Find the infinite sum of the geometric sequence with \( a=4, r=\frac{2}{8} \) if it exists. \[ S_{\infty}= \]

Answer 1

Answer: 16/3

Work Shown

The infinite geometric sum exists, i.e. the sum converges, because -1 < r < 1 is true here.

`S_(\infty) = (a)/(1-r)\\\\S_(\infty) = (4)/(1-(2/8))\\\\S_(\infty) = (4)/(1-(1/4))\\\\S_(\infty) = (4)/((4/4)-(1/4))\\\\S_(\infty) = (4)/((4-1)/4)\\\\S_(\infty) = (4)/(3/4)\\\\S_(\infty) = 4*(4/3)\\\\S_(\infty) = 16/3\\\\`

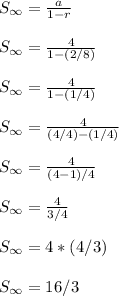
The geometric sequence {4, 1, 1/4, 1/16, 1/64, 1/256, 1/1024, 1/4096, 1/16384, ...} has the infinitely many terms sum to 16/3 = 5.33333.....

Here are a few partial sums:

• 4 + 1 = 5
• 4 + 1 + (1/4) = 5.25
• 4 + 1 + (1/4) + (1/16) = 5.3125
• 4 + 1 + (1/4) + (1/16) + (1/64) = 5.328125
• 4 + 1 + (1/4) + (1/16) + (1/64) + (1/256) = 5.33203125
• 4 + 1 + (1/4) + (1/16) + (1/64) + (1/256) + (1/1024) = 5.3330078125
• 4 + 1 + (1/4) + (1/16) + (1/64) + (1/256) + (1/1024) + (1/4096) = 5.333251953125
• 4 + 1 + (1/4) + (1/16) + (1/64) + (1/256) + (1/1024) + (1/4096) + (1/16384) = 5.33331298828125

The partial sums are slowly approaching 16/3 = 5.333333....

We'll never actually arrive at this exact value because we need infinitely many terms to do so.