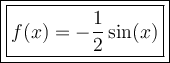Question

(50 POINTS PLEASE HELP)

Which function is shown on the graph? (picture attached)
f(x)=1/2sinx
f(x)=−1/2sinx
f(x)=−1/2cosx
f(x)=1/2cosx

Answer 1

`\textsf{b.} \quad f(x)=-(1)/(2)\sin(x)`

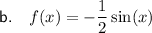
Explanation:

The given graph represents a sinusoidal wave that passes through the origin (0, 0), with a minimum value of -1/2 and a maximum value of 1/2.

The period of a sinusoidal graph represents the distance along the horizontal axis it takes for a sinusoidal wave to complete one full cycle and return to the same point on the graph. For this given graph, the period is 2π.

Since the parent function f(x) = sin(x) also passes through the origin and has a period of 2π, it is appropriate to use the parent function f(x) = sin(x) as the starting point to find the equation of the given graph.

The general equation of a sine function is:

`y=A\sin(B(x+C))+D`

where:

• A is the amplitude (height from the mid-line to the peak).
• 2π/B is the period (horizontal distance between consecutive peaks).
• C is the phase shift (horizontal shift - positive is to the left).
• D is the vertical shift.

In this case:

• The mid-line of the given graph is the x-axis, y = 0. The maximum value is y = 1/2, so the amplitude is A = 1/2.
• The period is 2π, so B = 1.
• The graph has no horizontal shift, so C = 0.
• The graph has no vertical shift, so D = 0.

Therefore, the equation of a function with these parameters is f(x) = (1/2)sin(x).

However, it is important to note that the graph of the parent sine function rises to its maximum value after passing through the origin, whereas the graphed function falls to its minimum value after passing through the origin. This indicates a reflection in the x-axis.

When we reflect a sinusoidal graph in the x-axis, we negate the function.

So, the equation of the graphed function, considering this reflection, is:

`\large\boxed{\boxed{f(x)=-(1)/(2)\sin(x)}}`