Question

Show that the set consisting of those numbers in (0,1) that have a decimal expansion containing one hundred consecutive 4 s is a Borel subset of R.

Answer 1

To show that the set consisting of numbers in (0,1) that have a decimal expansion containing one hundred consecutive 4s is a Borel subset of R, we can use the concept of Borel sets and the properties of decimal expansions.

Step-by-step explanation:

To show that the set consisting of numbers in (0,1) that have a decimal expansion containing one hundred consecutive 4s is a Borel subset of R, we can use the concept of Borel sets and the properties of decimal expansions.

A Borel set is a set that can be formed from open intervals using countable unions, intersections, and complements. Since the set in question can be described as the intersection of countably many open intervals, it is a Borel subset of R.

For example, one open interval that contains numbers with the decimal expansion 0.444... is (0.444... - ε, 0.444... + ε), where ε is a positive number smaller than 0.001 (to ensure the expansion contains one hundred 4s).

By taking the intersection of all such intervals for every possible decimal expansion with one hundred consecutive 4s, we form the Borel subset.

Answer 2

The set consisting of numbers in (0, 1) having a decimal expansion containing one hundred consecutive 4s is a Borel subset of R.

To show that the set A consisting of those numbers in the open interval (0, 1) that have a decimal expansion containing one hundred consecutive 4s is a Borel subset of R, we need to understand the concept of Borel sets and their properties.

A Borel set is any set that can be formed from open intervals using operations such as countable unions, countable intersections, and complements. The Borel σ-algebra on R is the smallest σ-algebra that contains all open intervals.

Let A be the set in question, defined as follows:

A = {x
`\in` (0, 1) | decimal expansion of x contains one hundred consecutive 4s}

We can express A as a countable union of open intervals.

Let
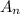`\(A_n\)` be the set of numbers in (0, 1) whose decimal expansion contains a sequence of n consecutive 4s. Then,

A =
`\bigcup_(n=1)^(\infty) A_(100)`

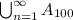
Each
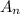`\(A_n\)` is an open set because, for each n, you can define an open interval around each such number that contains the sequence of n consecutive 4s. Since a countable union of open sets is a Borel set, A is a Borel set.

In conclusion, the set A is a Borel subset of R because it can be expressed as a countable union of open intervals, which generates a Borel set according to the definition of Borel sets.