For a Poisson distribution with
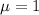 :
:
a.
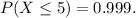
b.
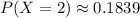 from formula and table.
from formula and table.
c.
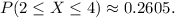
d. Probability
 exceeds its mean by more than one standard deviation:
exceeds its mean by more than one standard deviation:
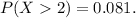
For a Poisson distribution with a mean
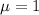 :
:
a. To find
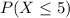 using Table A.2 (Poisson cumulative distribution table), locate the row for
using Table A.2 (Poisson cumulative distribution table), locate the row for
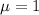 and find the corresponding value for
and find the corresponding value for
 . The value in the table represents
. The value in the table represents
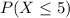 , which is approximately 0.999.
, which is approximately 0.999.
b. To determine
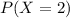 using the probability mass function (pmf) formula for the Poisson distribution:
using the probability mass function (pmf) formula for the Poisson distribution:
![\[P(X = k) = \frac{{e^(-\mu) \cdot \mu^k}}{{k!}}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ydzffnh1sx1y8efsai490zfaax6q6kfhng.png)
For
 and
and
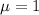 :
:
![\[P(X = 2) = \frac{{e^(-1) \cdot 1^2}}{{2!}} = \frac{{e^(-1)}}{{2}} \approx 0.1839\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6wrw3pmn3sqanhblz3323ggtro4ymhmait.png)
You can also verify this value using Table A.2, where the row for
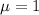 and column for
and column for
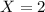 gives approximately
gives approximately
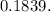
c. To find
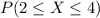 , you can sum the individual probabilities
, you can sum the individual probabilities
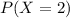 ,
,
 , and
, and
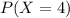 using the Poisson pmf formula:
using the Poisson pmf formula:
![\[P(X = 3) = \frac{{e^(-1) \cdot 1^3}}{{3!}} = \frac{{e^(-1)}}{{6}} \approx 0.0613\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pigrgu0qnym072urd6fctkti2b1ejfdj74.png)
![\[P(X = 4) = \frac{{e^(-1) \cdot 1^4}}{{4!}} = \frac{{e^(-1)}}{{24}} \approx 0.0153\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/c2zemx6lz9dhy2sl5hrgg5jy4zxbo9juw3.png)
Therefore,
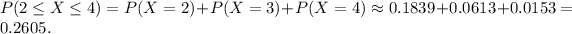
d. The standard deviation of a Poisson distribution is
 . For
. For
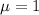 , the standard deviation
, the standard deviation
 is
is
 .
.
The probability that \(X\) exceeds its mean value by more than one standard deviation is the probability of
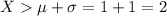 . This is the same as finding
. This is the same as finding
 .
.
![\[P(X > 2) = 1 - P(X \leq 2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yaer28qdwmmfmnaeylcww0lvpfvshlp8ku.png)
Using Table A.2 for
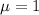 and
and
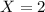 ,
,

So
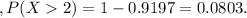
complete the question
The article "Expectation Analysis of the Probability of Failure for Water Supply Pipes" (J. of Pipeline Systems Engr. and Practice, May 2012: 36-46) pro- posed using the Poisson distribution to model the num- ber of failures in pipelines of various types. Suppose that for cast-iron pipe of a particular length, the expected number of failures is 1 (very close to one of the cases considered in the article). Then X, the number of failures, has a Poisson distribution with μ = 1.
a. Obtain P(X ≤5) by using Appendix.
b. Determine P(X=2) first from the pmf formula and then from Appendix Table A.2.
c. Determine P(2 ≤ X ≤ 4).
d. What is the probability that X exceeds its mean value by more than one standard deviation?