Final answer:
To solve the equation
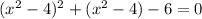 , we can simplify the expression inside the parentheses and combine like terms to get a fourth-degree polynomial equation.
, we can simplify the expression inside the parentheses and combine like terms to get a fourth-degree polynomial equation.
Step-by-step explanation:
To solve the equation
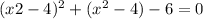 , we can start by simplifying the expression inside the parentheses. Using the exponent rule (a-b)2 = a2 - 2ab + b2, we have
, we can start by simplifying the expression inside the parentheses. Using the exponent rule (a-b)2 = a2 - 2ab + b2, we have
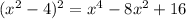 . Substituting this back into the equation gives us
. Substituting this back into the equation gives us
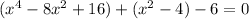 . Combining like terms, we get
. Combining like terms, we get
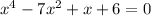 . This is a fourth-degree polynomial equation that can be solved using factoring, the quadratic formula, or other methods.
. This is a fourth-degree polynomial equation that can be solved using factoring, the quadratic formula, or other methods.
Learn more about Solving polynomial equations