Question

Ashlyn had some Barbie dolls. Joslyn has 78 barbies. Rounded to the nearest ten, together they have 140 Barbie dolls. How many do Ashlyn has?​

Answer 1

Answer: Somewhere between 57 and 66 barbie dolls. Include both endpoints.

Explanation

x = total number of barbie dolls

When rounding x to the nearest ten, we get 140.

Because x is a positive whole number, the smallest x could be is 135 and the largest is 144.

`135 \le \text{x} \le 144`

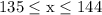
x is between 135 and 144 including both endpoints.

Subtract 78 from all sides

`135 \le \text{x} \le 144\\\\135-78 \le \text{x}-78 \le 144-78\\\\57 \le \text{x}-78 \le 66\\\\`

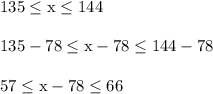
x is the total number of dolls, 78 is the number Joslyn has, and x-78 is the number Ashlyn has.

We don't know the exact number Ashlyn has, but we do know the range of values. Her count is somewhere between 57 and 66 including both endpoints.

------------

Example:

• Ashlyn has 60 dolls
• Joslyn has 78 dolls
• 60+78 = 138 total

That rounds to 140 when rounding to the nearest ten.

------------

Another Example:

• Ashlyn has 63 dolls
• Joslyn has 78 dolls
• 60+78 = 141 total

That rounds to 140 when rounding to the nearest ten.

------------

Something that does NOT work:

• Ashlyn has 100 dolls
• Joslyn has 78 dolls
• 100+78 = 178 total

That rounds to 180 when rounding to the nearest ten. This total is too large even before rounding.

Answer 2

62 Barbie dolls

Explanation:

Let's say Ashlyn has a variable number of barbies, let's call it a.

We know that Joslyn has 78 barbies, and that together they have 140 barbies rounded to the nearest ten.

We can set up an equation to represent this:

`\sf a + 78 = 140`

Subtracting 78 from both sides of the equation, we get:

`\sf a+78-78 =140-78`

`\sf a = 62`

Therefore, Ashlyn has 62 Barbie dolls.