Question

Prove each of the following statements: For any integer n, if n³ +1 is even n is odd. Solution:

Answer 1

The claim is true

Proof by contrapositive.

The conditional "if P, then Q" has the contrapositive "if not Q, then not P".

We negate each part and swap them.

An example would be "if it rains, then it's wet outside" has the contrapositive "if it's not wet outside, then it's not raining".

The conditional
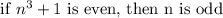`\text{ if } n^3+1 \text{ is even, then n is odd}` has the contrapositive form
`\text{ if n is not odd, then } n^3+1 \text{ is not even}`

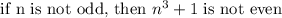
We can rewrite that to
`\text{ if n is even, then } n^3+1 \text{ is odd}`

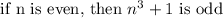
Assume n is even. This would mean n = 2k for some integer k.

`n^3+1 = (2k)^3+1\\\\n^3+1 = 8k^3+1\\\\n^3+1 = 2(4k^3)+1\\\\n^3+1 = 2(\text{some integer})+1\\\\n^3+1 = \text{some odd integer}`

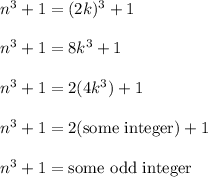
Therefore, if n is even, then
`n^3+1` is odd.

This wraps up the contrapositive proof. This is because the original conditional and the contrapositive form have the same truth value. If one is true then both are true.

-----------------------------

Another Proof:

Let
`n^3+1` be an even integer.

`n^3+1 = 2m, \ \text{ for some integer m}`

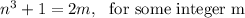
Subtract 1 from both sides to get
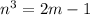`n^3 = 2m-1` which is odd. The 2m is even and 2m-1 is odd.

If n was even, then
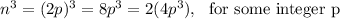`n^3 = (2p)^3 = 8p^3 = 2(4p^3), \ \text{ for some integer p}` which shows that
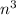`n^3` is also even.

But this contradicts the
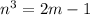`n^3 = 2m-1` being odd.

Therefore n must be odd when
`n^3+1` is even.