Question

An insurance company found that 24% of male drivers between the ages of 18 and 25 are involved in serious accidents annually. To simplify the analysis assume that every such accident costs the insurance company $64,000 and that a driver can only have one of those accidents in a year Completo parts (a) through (c) (a) If the company charges $2,600 for such coverage, what is the chance that it losos money on a single policy? Piloses money) - 1024 (Type an integer or a decimal) (6) Suppose that the company writes 1.000 such policies to a collection of drivers. What is the probability that the company make a profit on those policies? Assume that the drivers don't run into each other and behave independently P(profit) = (Round to five decimal places as needed)

Answer 1

The chance that the insurance company loses money on a single policy is 24.62%. The probability that the company makes a profit on a collection of policies is 75.38%.

Step-by-step explanation:

To determine the chance that the insurance company loses money on a single policy, we need to compare the cost of the accidents to the premium charged. The company charges $2,600 for coverage and each accident costs $64,000. So, the chance that the company loses money on a single policy is given by the ratio of the accident cost to the premium:

`P(loses money) = (64,000)/(2,600)`

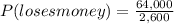
Therefore, P(loses money) = 24.62

For part (b), since each policy is independent, we can use the probability of losing money on a single policy to find the probability of making a profit on a collection of policies. The probability of making a profit on those policies is given by 1 minus the probability of losing money on a single policy:

P(profit) = 1 - P(loses money) = 1 - 0.2462

Therefore, P(profit) = 0.7538