Question

Find a particular solution to the differential equation -9y" + 0y' + 1y = -1t^2 + 1t + 3e^3t

Answer 1

The particular solution to the differential equation -9y" + 0y' + 1y = -1t^2 + 1t + 3e^3t can be found using the method of undetermined coefficients, assuming the form At^2 + Bt + C for the polynomial and De^3t for the exponential term, and then solving for constants A, B, C, and D.

Step-by-step explanation:

To find a particular solution to the differential equation -9y" + 0y' + 1y = -1t^2 + 1t + 3e^3t, we will use the method of undetermined coefficients. Since the differential equation is linear and the right-hand side is a polynomial plus an exponential function, the particular solution will take the form of a polynomial plus an exponential term.

The polynomial part to fit -1t^2 + 1t can be assumed as At^2 + Bt + C. Given e^3t is not a solution to the homogeneous equation, we can assume an exponential particular solution of the form De^3t.

Inserting our assumed particular solution into the differential equation gives a system of equations from which we can solve for constants A, B, C, and D. This provides us with a specific form of the particular solution.

Answer 2

`\[ y_p(t) = (1)/(18)t^2 + t - (1)/(27)e^(3t) \]` is the particular solution of the differential equation
`\[ -9y'' + 0y' + y = -t^2 + t + 3e^(3t) \]`.

Given:

`\[ -9y'' + 0y' + y = -t^2 + t + 3e^(3t) \]`

To find a particular solution to the given second-order linear differential equation, we can use the method of undetermined coefficients. The general form of the particular solution is assumed to have the same form as the non-homogeneous term, with undetermined coefficients. In this case, we have a non-homogeneous term of the form:

`\[ g(t) = -t^2 + t + 3e^(3t) \]`

Let's assume the particular solution has the form:

`\[ y_p(t) = At^2 + Bt + Ce^(3t) \]`

Now, we'll find the first and second derivatives of
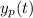`\(y_p(t)` and substitute them into the differential equation:

`\[ y_p(t) = At^2 + Bt + Ce^(3t) \]`

`\[ y_p'(t) = 2At + B + 3Ce^(3t) \]`

`\[ y_p''(t) = 2A + 9Ce^(3t) \]`

Substituting the values:

`\[ -9(2A + 9Ce^(3t)) + 0(2At + B + 3Ce^(3t)) + (At^2 + Bt + Ce^(3t)) = -t^2 + t + 3e^(3t) \]`

Simplify and equate coefficients:

`\[ -18A - 81Ce^(3t) + Bt + Ce^(3t) = -t^2 + t + 3e^(3t) \]`

Now, equate coefficients for each term:

Coefficient of
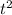`\(t^2`: -18 A = -1
`\(\Rightarrow \) \(A = (1)/(18) \)`

Coefficient of t: B = 1 (no t term on the right side)

Coefficient of
`\(e^(3t)\)`: -81 C = 3
`\(\Rightarrow \) \(C = -(1)/(27) \)`

So, the particular solution is:

`\[ y_p(t) = (1)/(18)t^2 + t - (1)/(27)e^(3t) \]`

This is a particular solution to the given differential equation.