Question

Compute the doubling time (in years) associated to an annual compound interest rate of 6.5%.

Answer 1

11 years

Explanation:

Formula for annual compound interest:
`A=P(1+r)^t`. In context of this problem, P and A are not relevant as they aren't mentioned. So, the equation we want to end up solving is
`2=(1+r)^t`, where t is the unknown variable we're solving for, and r = .065. We desire to double the amount, A, so the left side of the equation is set to 2.

1. Set up the equation:
   
   `2=(1+.065)^t\\ > 2=1.065^t`

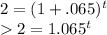
• To solve this, you should know the format of a basic logarithm:
  
  `b^x=a < - > log_(b)a=x`.

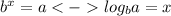2. Set up the logarithm and solve:

• 
  
  `1.065^t=2\\log_(1.065)(2)=t\\t= 11.00673904`

t = 11 years

As a side note that may be irrelevant if this is a math course, economists often use the "rule of 72" for compound interest doubling time. Meaning
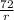`(72)/(r)` returns the doubling time in years. 72/6.5 gives us ≈ 11.079, or 11 years as well.