Answer:
Overview of proof (by contradiction):
- Assume by contradiction it takes more than
 steps to reach
steps to reach
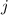 from
from
 .
. - By assumption, the shortest path from
 to
to
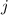 should includes more than
should includes more than
 steps.
steps. - Apply the pigeonhole principle to demonstrate that at least one state will be repeated along this path, forming a loop.
- Define a new path from the original path, bypassing the loop.
- Notice that this new path still goes from
 to
to
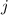 . However, unlike the original path, this new path is strictly shorter because it skipped the loop.
. However, unlike the original path, this new path is strictly shorter because it skipped the loop. - Arrive at a contradiction with the previous assumption: the original path isn't the shortest from
 to
to
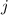 .
.
Step-by-step explanation:
Since state
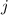 is accessible from state
is accessible from state
 , there exists a path
, there exists a path
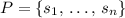 where
where
 and
and
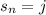 . For
. For
 to be a valid path,
to be a valid path,
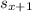 must be a neighbor of
must be a neighbor of
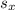 for each integer
for each integer
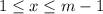 . Notice that there are
. Notice that there are
 states in path
states in path
 , meaning that it would take
, meaning that it would take
 steps to go from
steps to go from
 to
to
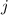 following this path.
following this path.
Assume by contradiction it takes strictly more than
 steps to go from state
steps to go from state
 to state
to state
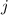 . In other words, any path that goes from state
. In other words, any path that goes from state
 to state
to state
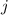 should include at least
should include at least
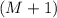 states.
states.
Let
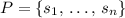 be the shortest path from state
be the shortest path from state
 to state
to state
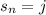 . Under the assumption,
. Under the assumption,
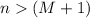 .
.
Note that the number of states visited in
 exceeds the total number of states in this Markov chain:
exceeds the total number of states in this Markov chain:
 . By the pigeonhole principle, it is not possible to define an injective map from
. By the pigeonhole principle, it is not possible to define an injective map from
 to the set of states
to the set of states
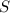 because
because
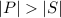 . In simpler words, at least one state in this Markov chain is repeated in the list of states visited along path
. In simpler words, at least one state in this Markov chain is repeated in the list of states visited along path
 .
.
Assume that the
 th state
th state
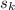 in path
in path
 is repeated. There would exist an integer
is repeated. There would exist an integer
 (
(
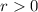 ) such that
) such that
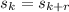 :
:
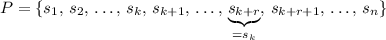 .
.
Notice that
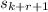 is a neighbor of
is a neighbor of
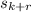 . However, because
. However, because
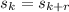 ,
,
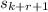 is also a neighbor of
is also a neighbor of
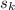 . The following would also be a valid path between
. The following would also be a valid path between
 and
and
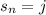 .:
.:
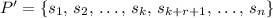 .
.
However, path
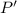 contains
contains
 fewer steps than path
fewer steps than path
 . This observation is a contradiction of the previous assumption that path
. This observation is a contradiction of the previous assumption that path
 is the shortest path from state
is the shortest path from state
 to state
to state
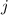 .
.
In simpler words, between step
 and step
and step
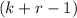 , the original path
, the original path
 went through a loop of
went through a loop of
 steps (
steps (
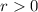 ) that eventually goes back to
) that eventually goes back to
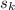 . Skipping this loop creates a new path
. Skipping this loop creates a new path
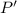 , which is also a valid path between
, which is also a valid path between
 and
and
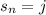 . However, the new path would be strictly shorter than the original path, which leads to a contradiction.
. However, the new path would be strictly shorter than the original path, which leads to a contradiction.