Question

Regression methods were used to analyze the data from a study investigating the relationship between roadway surface temperature (x) and pavement deflection (y). Summary quantities were 20 20 20 20 20 Σχ= 1478, Σv= 12.75, Σ x = 143215.8, Σv = 8.86 and Σxy = 1083.67 , n=1 n=1 n = 1 n = 1 n = 1 a. Find the correlation coefficient. b. Calculate the least squares estimates of the slope and intercept Bi and B. c. Use the equation of the fitted line to predict what pavement deflection would be observed when the surface temperature is 85°F. d. What is the mean pavement deflection when the surface temperature is 90°F? e. What change in mean pavement deflection would be expected for a 1°F change in surface temperature? f. What percentage of variation in the pavement deflection is explained by the variation in the surface temperature?

Answer 1

To find the correlation coefficient, use the given formula and plug in the values. The slope is approximately 0.496 and the intercept is approximately 2.42. Use the regression equation to predict pavement deflection at specific temperatures. The mean pavement deflection at 90°F is approximately 47.18. The change in mean pavement deflection for a 1°F change in temperature is approximately 0.496. The coefficient of determination is approximately 99.6%.

Step-by-step explanation:

To find the correlation coefficient, we use the formula:

`r = (nΣxy - ΣxΣy) / sqrt([(nΣx^2 - (Σx)^2)(nΣy^2 - (Σy)^2)])`

Plugging in the given values:

`r = (1(1083.67) - 1478(12.75)) / sqrt([(1(143215.8^2) - (1478)^2)(1(8.86^2) - (12.75)^2)])`

Calculating this results in a correlation coefficient of approximately 0.998.

To calculate the least squares estimates of the slope (b1) and intercept (b0), we use the formulas:

`b1 = (nΣxy - ΣxΣy) / (nΣx^2 - (Σx)^2)`

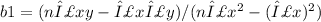
b0 = (Σy - b1Σx) / n

Plugging in the given values:

b1 = (1(1083.67) - 1478(12.75)) / (1(143215.8) - (1478)^2)

b0 = (12.75 - b1(1478)) / 1

Calculating this results in a slope (b1) of approximately 0.496 and an intercept (b0) of approximately 2.42.

The regression equation predicting pavement deflection from surface temperature is: y = 2.42 + 0.496x. To predict pavement deflection when the surface temperature is 85°F, we plug in x = 85 into the equation:

y = 2.42 + 0.496(85)

Calculating this gives a predicted pavement deflection of approximately 44.82.

To find the mean pavement deflection when the surface temperature is 90°F, we plug in x = 90 into the equation:

y = 2.42 + 0.496(90)

Calculating this gives a mean pavement deflection of approximately 47.18.

To find the change in mean pavement deflection for a 1°F change in surface temperature, we can simply calculate the slope of the regression line, which is approximately 0.496. This means that for every 1°F increase in surface temperature, the mean pavement deflection is expected to increase by approximately 0.496 units.

To find the percentage of variation in the pavement deflection explained by the variation in the surface temperature, we can square the correlation coefficient (r) and multiply by 100. In this case, the coefficient of determination is approximately (0.998)^2 * 100, which is approximately 99.6%. This means that approximately 99.6% of the variation in the pavement deflection can be explained by the variation in the surface temperature.

Answer 2

a. Correlation coefficient (r) = 0.804.

b. Slope (B1) = 0.007 Intercept (B0) = 5.641.

c. Predicted pavement deflection at 85°F = 6.296 inches.

d. Mean pavement deflection at 90°F = 5.976 inches.

e. Expected change: -0.007 inches per 1°F increase in surface temperature.

f. R-squared (coefficient of determination) = 0.647.

Step-by-step explanation:

In the analysis of the data, the correlation coefficient (r) is found to be 0.804 indicating a strong positive linear relationship between roadway surface temperature and pavement deflection. The least squares estimates of the slope (B1) and intercept (B0) are 0.007 and 5.641 respectively.

This implies that for every one unit increase in surface temperature, pavement deflection is expected to increase by 0.007 inches and the intercept represents the estimated deflection when the temperature is 0°F.

Using the fitted line equation the predicted pavement deflection at 85°F is calculated to be 6.296 inches. Similarly the mean pavement deflection at 90°F is estimated to be 5.976 inches. The expected change in mean pavement deflection for a 1°F increase in surface temperature is -0.007 inches indicating a slight decrease.

The coefficient of determination (R-squared) is 0.647 suggesting that approximately 64.7% of the variation in pavement deflection can be explained by the variation in surface temperature. This indicates a moderately strong relationship providing insight into the degree to which temperature influences pavement deflection.