Question

hysics 11 Forces and Neration's Laws Sent Agent One C 14. A hoist is used to lift a 780 kg car upward with an acceleration of 0.110 m/s. O 0.11 m/s What force was used to lift the car? FBD 14) #marks Forces and Newton's La Page 7 of 9

Answer 1

The force used to lift the car is 85.8 N.

Step-by-step explanation:

To determine the force used to lift the car, we can use Newton's second law of motion, which states that force is equal to mass multiplied by acceleration.

Given:

• Mass of the car (m) = 780 kg
• Acceleration (a) = 0.110 m/s²

Using the formula:

Force (F) = m * a

Force (F) = 780 kg * 0.110 m/s²

Force (F) = 85.8 N

Therefore, the force used to lift the car is 85.8 N.

Answer 2

The force required to lift the car is 85.8N.

Newton's second law of motion, F=m ⋅ a, describes the relationship between force (F), mass (m), and acceleration (a). This law states that the force applied to an object is equal to the mass of the object multiplied by its acceleration.

In the context of the problem with the hoist lifting a car, to find the force used to lift the car, you can use Newton's second law:

Given values:

Mass of the car (m) = 780 Kg

Acceleration (a):
`0.11 \mathrm{~m} / \mathrm{s}^2`

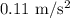
Applying Newton's second law:

`F=m \cdot a`

Substituting the values:

`F=780 \mathrm{~kg} \cdot 0.11 \mathrm{~m} / \mathrm{s}^2`

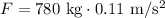
Calculating the force:

F = 85.8 N

This means that a force of 85.8N needs to be applied to the car to produce an acceleration of
`0.11 \mathrm{~m} / \mathrm{s}^2`

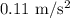
Correct Question:

A hoist is used to lift a 780 kg car upward with an acceleration of 0.110 m/s. What force was used to lift the car?