Question

MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER The rate of depreciation dv/dt of a machine is inversely proportional to the square of t + 1, where V is the value of the machine t years after it was purchased. The initial value of the machine was $900,000, and its value decreased $200,000 in the first year. Estimate its value after 5 years. (Round your answer to the nearest whole number.)

Answer 1

The initial value of the machine is $900,000, and after one year, it depreciated by $200,000. By integrating the given rate of depreciation inversely proportional to the square of (t + 1), we can calculate the constant of proportionality and estimate the machine's value after 5 years.

Step-by-step explanation:

The depreciation rate (dv/dt) of a machine is given as inversely proportional to the square of (t + 1). This can be represented mathematically as dv/dt = k/(t + 1)², where k is the constant of proportionality. Given that the initial value (V0) is $900,000 and in the first year the value decreased by $200,000, we can calculate the constant k using the change in value and time period.

To estimate the value after 5 years, we integrate the equation dv = k/(t + 1)² dt from t = 0 to t = 5, using the boundary condition that V = 900,000 when t = 0. Calculate the integral to find the expression for V as a function of t, and then substitute t = 5 to find the estimated value of the machine after 5 years.

Using the information that V decreased by $200,000 after the first year, we have the equation 700,000 = 900,000 - k ∫_{0}^{1} dt/(t + 1)². Solving this we find the value of k. Now, to find the value of the machine after 5 years, let's assume V(5) = 900,000 - k ∫_{0}^{5} dt/(t + 1)². We evaluate this integral to get the estimate.

Answer 2

Rounded to the nearest whole number, the estimated value of the machine after 5 years is $1,566,667.

Given that the rate of depreciation
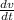`\( (dv)/(dt) \)` of a machine is inversely proportional to the square of t + 1, where V is the value of the machine t years after it was purchased, we have the relation:

`\[ (dv)/(dt) = k \cdot \frac{1}{{(t+1)}^2} \]`

Where:

- V is the value of the machine at time t

- t is the time in years after the machine was purchased

- k is a constant of proportionality

Given that the initial value of the machine was $900,000 and it decreased $200,000 in the first year, we can use this information to estimate the value of k.

Let's set up the initial conditions:

-
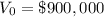`\( V_0 = \$900,000 \)` (initial value)

-
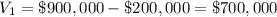`\( V_1 = \$900,000 - \$200,000 = \$700,000 \)` (value after the first year when t = 1

Using this information, we can solve for k by substituting these values into the equation:

`\[ (dv)/(dt) = k \cdot \frac{1}{{(t+1)}^2} \]`

At t = 1:

`\[ (dv)/(dt) = k \cdot \frac{1}{{(1+1)}^2} \]`

`\[ (dv)/(dt) = k \cdot (1)/(4) \]`

Given that
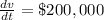`\( (dv)/(dt) = \$200,000 \)` (decrease in value in the first year), we can solve for k:

`\[ \$200,000 = k \cdot (1)/(4) \]`

`\[ k = \$200,000 * 4 = \$800,000 \]`

Now, with the value of k, we can proceed to estimate the value of the machine after 5 years. We'll integrate the equation:

`\[ (dv)/(dt) = \$800,000 \cdot \frac{1}{{(t+1)}^2} \]`

Integrating this gives:

`\[ V = -\$800,000 \cdot \frac{1}{{t+1}} + C \]`

Given the initial value of the machine
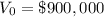`\( V_0 = \$900,000 \)`, substitute t = 0 and solve for C:

`\[ \$900,000 = -\$800,000 \cdot \frac{1}{{0+1}} + C \]`

`\[ \$900,000 = -\$800,000 + C \]`

`\[ C = \$1,700,000 \]`

Now, for t = 5:

`\[ V = -\$800,000 \cdot \frac{1}{{5+1}} + \$1,700,000 \]`

`\[ V = -\$800,000 \cdot (1)/(6) + \$1,700,000 \]`

`\[ V = -\$133,333.33 + \$1,700,000 \]`

`\[ V \approx \$1,566,666.67 \]`