Question

Need help please

The first difference of a sequence is 2,5,8,11,14, ... Find the first six terms of the original sequence in each of the following cases.
a. The first term of the original sequence is 3.
b. The sum of the first two terms in the original sequence is 12.
c. The fifth term in the original sequence is 34.

a. The first six terms are | |, | |, | |, | |, | |, and | |.
(Simplify your answers. Use ascending order.)

Answer 1

(a) 3, 5, 10, 18, 29, 43

(b) 5, 7, 12, 20, 31, 45

(c) 8, 10, 15, 23, 34, 48

Explanation:

The first differences of a sequence are the values obtained by subtracting one term in the sequence from the next term.

If the first differences of a sequence are 2, 5, 8, 11, and 14, then:

`a_1\underset{+2}{\longrightarrow}a_2\underset{+5}{\longrightarrow}a_3\underset{+8}{\longrightarrow}a_4\underset{+11}{\longrightarrow}a_5\underset{+14}{\longrightarrow}a_6`

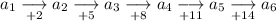
where
`a_n` is the nth term of the sequence.

`\hrulefill`

Part (a)

Starting with the first term (a₁) of the original sequence as a₁ = 3, we can find the next terms by adding the given differences successively:

`3\underset{+2}{\longrightarrow}5\underset{+5}{\longrightarrow}10\underset{+8}{\longrightarrow}18\underset{+11}{\longrightarrow}29\underset{+14}{\longrightarrow}43`

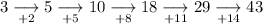
Therefore, the first six terms of this sequence are:

• 3, 5, 10, 18, 29, 43

`\hrulefill`

Part (b)

If the sum of the first two terms is 12, then:

`a_1 + a_2 = 12`

As the difference between the first and second terms is 2, to find the second term in the sequence, we simply add 2 to the first term:

`a_2 = a_1 + 2`

Substituting this into the previous equation we get:

`a_1 + a_1 + 2 = 12`

Solve for a₁:

`2a_1 + 2 = 12`

`2a_1 =10`

`a_1 =5`

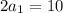
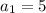
Therefore, as the first term (a₁) is 5, substitute a₁ = 5 into the sequence and add the given differences successively:

`5\underset{+2}{\longrightarrow}7\underset{+5}{\longrightarrow}12\underset{+8}{\longrightarrow}20\underset{+11}{\longrightarrow}31\underset{+14}{\longrightarrow}45`

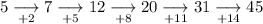
Therefore, the first six terms of this sequence are:

• 5, 7, 12, 20, 31, 45

`\hrulefill`

Part (c)

If the fifth term of the original sequence is 34, then a₅ = 34:

`a_1\underset{+2}{\longrightarrow}a_2\underset{+5}{\longrightarrow}a_3\underset{+8}{\longrightarrow}a_4\underset{+11}{\longrightarrow}34\underset{+14}{\longrightarrow}a_6`

To find the previous term in the sequence, we need to subtract the difference each time. To find the last term of the sequence, add 14 to the fifth term:

`8\underset{+2}{\longrightarrow}10\underset{+5}{\longrightarrow}15\underset{+8}{\longrightarrow}23\underset{+11}{\longrightarrow}34\underset{+14}{\longrightarrow}48`

Therefore, the first six terms of this sequence are:

• 8, 10, 15, 23, 34, 48