Question

7. A Ferris wheel has a diameter of 60 metres. It rotates once every 48 seconds. Riders must climb up 2 meters to get on the ride. Andrew gets on the Ferris wheel at its lowest point and then the wheel starts to rotate. a) Sketch the sinusoidal graph that models Andrew's height h (in metres) above the ground as a function of the elapsed time t (in seconds). Determine a cosine equation. (2 marks] b) Determine the time when Andrew will be 38 metres above the ground in the first rotation of the Ferris wheel. [3 marks]

Answer 1

The final answer is that Andrew will be approximately 38 meters above the ground after approximately 7.245 seconds from the time he boards the Ferris wheel at its lowest point, within the first rotation.

a) To model Andrew's height above the ground as a function of time, we can use a cosine function because it starts at the lowest point and moves upwards. The general form of a cosine function is:

`\[h(t) = A \cos(B(t - C)) + D\]`

Where:

- A is the amplitude (half of the vertical distance between the maximum and minimum)

- B affects the period of the function:
`\(B = \frac{2\pi}{\text{period}}\)`

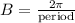
- C is the phase shift (horizontal shift)

- D is the vertical shift (in this case, the initial height)

Given:

- Diameter of Ferris wheel = 60 meters (Radius = 30 meters)

- Riders climb up 2 meters to get on the ride

The amplitude A is half the diameter of the wheel since it goes from the lowest point to the highest point, which is 30 + 2 = 32 meters.

The period of a full rotation is the time taken to complete one full cycle, which is 48 seconds.

The cosine function for Andrew's height h(t) will start at the lowest point, so there is no phase shift (C = 0). The initial height is 2 meters above the lowest point (D = 2).

Therefore, the equation for Andrew's height h(t) is:

`\[h(t) = 32 \cos\left((2\pi)/(48)t\right) + 2\]`

b) To find when Andrew will be 38 meters above the ground, set h(t) = 38 and solve for t:

`\[38 = 32 \cos\left((2\pi)/(48)t\right) + 2\]`

Subtract 2 from both sides:

`\[36 = 32 \cos\left((2\pi)/(48)t\right)\]`

Now, isolate the cosine term:

`\[\cos\left((2\pi)/(48)t\right) = (36)/(32) = (9)/(8)\]`

Next, solve for t by taking the inverse cosine (arccosine) of both sides:

`\[(2\pi)/(48)t = \arccos\left((9)/(8)\right)\]`

Now, solve for t:

`\[t = (48)/(2\pi) \cdot \arccos\left((9)/(8)\right)\]`

As,
`\[\arccos\left((9)/(8)\right) \approx 0.451\text{ radians}\]`

Now, substitute this value into the equation:

`\[t = (48)/(2\pi) * 0.451 \approx 7.245 \text{ seconds}\]`

Therefore, Andrew will be approximately 38 meters above the ground after about 7.245 seconds from the time he boards the Ferris wheel at its lowest point, within the first rotation.