Question

The equation (x + 1)² - 6(x + 1) + 8 = 0 is of quadratic quadratic equation is ² 6w+8+ = 0 X type. To solve the equation, we set W = x +1​

Answer 1

Answers: x = 1 and x = 3

Step-by-step explanation

Replacing every (x+1) with variable w gets us
`w^2-6w+8 = 0`

The coefficients from left to right are: a = 1, b = -6, c = 8

Plug those into the quadratic formula.

`w = (-b\pm√(b^2-4ac))/(2a)\\\\w = (-(-6)\pm√((-6)^2-4(1)(8)))/(2(1))\\\\w = (6\pm√(36-32))/(2)\\\\w = (6\pm√(4))/(2)\\\\w = (6\pm2)/(2)\\\\w = (6+2)/(2) \ \text{ or } \ w = (6-2)/(2)\\\\w = (8)/(2) \ \text{ or } \ w = (4)/(2)\\\\w = 4 \ \text{ or } \ w = 2\\\\`

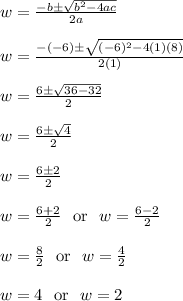
Or an alternative route is to factor like so:

`w^2 - 6w + 8 = 0\\\\(w-4)(w-2) = 0\\\\w-4 = 0 \ \text{ or } \ w-2 = 0\\\\w = 4 \ \text{ or } \ w = 2\\\\`

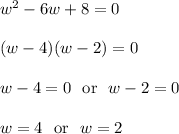
Factoring won't always work. Because factoring is a trial-and-error process, the quadratic formula is the most efficient route.

---------------

After we determine the values for w, let's solve for x.

If w = 4, then,

w = x+1

x = w-1

x = 4-1

x = 3

If w = 2, then,

x = w-1

x = 2-1

x = 1

Therefore, the solutions to
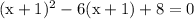`(\text{x}+1)^2 - 6(\text{x}+1) + 8 = 0` are x = 1 and x = 3