Question

What is the leading coefficient in the polynomial: 4x-3x^2+10x-x-12+7x^2+5

Answer 1

4 is the leading coefficient

When you combine like terms the polynomial is;
4x^2 + 13x -7

Answer 2

4

Explanation:

The leading coefficient of a polynomial is the coefficient of the term with the highest degree. The degree of a term is the exponent of the variable in that term.

In order to find the leading coefficient in a polynomial, we need to identify the term with the highest degree, and the coefficient of that term is the leading coefficient.

In the given polynomial:

`\sf 4x - 3x^2 + 10x - x - 12 + 7x^2 + 5`

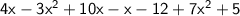
The terms with the highest degree are the ones with:

`\sf x^2, \textsf{ which are } -3x^2 \textsf{ and } 7x^2`

To find the leading coefficient, we need to sum the coefficients of these terms:

`\sf -3x^2 + 7x^2 = 4x^2`

So, the leading coefficient in the polynomial is 4.