Question

A certificate of deposit (CD) is a savings instrument that many banks offer. It usually gives a higher interest rate, but you cannot access your investment for a specified length of time. Suppose you deposit $3000 in a CD paying 4% interest, compounded monthly. How much will you have in the account after 20 years? Round your answer to the nearest cent.

Answer 1

To calculate the future value of a $3000 CD at a 4% interest rate, compounded monthly for 20 years, use the compound interest formula, which results in an amount of $6,609.12 after 20 years.

Step-by-step explanation:

The question posed by the student involves calculating the future value of an investment in a certificate of deposit (CD) that compounds interest monthly. To determine how much will be in the account after 20 years when you invest $3000 at a 4% annual interest rate, compounded monthly, you would use the compound interest formula:

`A = P(1 + r/n)^{(nt)`

Where:

• A is the amount of money accumulated after n years, including interest.
• P is the principal amount (the initial amount of money).
• r is the annual interest rate (decimal).
• n is the number of times that interest is compounded per year.
• t is the time the money is invested for, in years.

Plugging in the values:

`A = $3000(1 + 0.04/12)^{(12*20)`

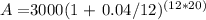
After calculating and rounding to the nearest cent:

A = $6,609.12

Therefore, after 20 years, the account will have $6,609.12

Answer 2

After 20 years, you will have approximately $6555.05 in the account, rounded to the nearest cent.

The formula to calculate the future value of an investment with compound interest is given by:

`\[ A = P * \left(1 + (r)/(n)\right)^(n * t) \]`

Where:

- A is the future value of the investment.

- P is the principal amount (initial deposit) - $3000 in this case.

- r is the annual interest rate (as a decimal) - 4% or 0.04.

- n is the number of times the interest is compounded per year - monthly compounding means n = 12.

- t is the time the money is invested for - 20 years in this case.

Let's plug in the values and calculate:

`\[ A = 3000 * \left(1 + (0.04)/(12)\right)^(12 * 20) \]`

`\[ A = 3000 * \left(1 + (0.04)/(12)\right)^(240) \]`

Using a calculator:

`\[ A \approx 3000 * (1.003333)^(240) \]`

`\[ A \approx 3000 * 2.191684 \]`

`\[ A \approx 6555.05 \]`