Question

A rural mail carrier is driving slowly, putting mail in mailboxes near the road. He overshoots one mailbox, stops, shifts into reverse, and then backs up until he is at the right spot. The velocity graph given below represents his motion. a. Draw the mail carrier's position vs. time graph. Assume that x = 0 m at t = 0 s. A. [Depiction of the position vs. time graph] B. [Another depiction of the position vs. time graph] C. [Yet another depiction of the position vs. time graph] D. [One more depiction of the position vs. time graph] What is the position of the mailbox? A. 0 m B. 4 m C. 8 m D. 12 m

Answer 1

The position of the mailbox is 12 m. The mail carrier's position vs. time graph is a straight line with a positive slope for the first 3 seconds, followed by a flat line. So, the option D is correct.

Step-by-step explanation:

Creating the mail carrier's position vs. time graph involves interpreting the provided velocity graph.

The position graph is derived from the integral of the velocity graph, starting at the origin (x = 0 m, t = 0 s).

Initially, the mail carrier maintains a constant velocity of 4 m/s for the initial 3 seconds, resulting in a linear increase in position from 0 to 12 m.

After the first 3 seconds, the mail carrier changes direction, exhibiting a constant velocity of -4 m/s for the subsequent 3 seconds.

During this interval, the position graph remains flat, indicating a constant position at 12 m.

In summary, the mail carrier's position vs. time graph features an ascending linear segment with a slope of 4 m/s for the first 3 seconds, succeeded by a horizontal segment depicting a constant position of 12 m for the subsequent 3 seconds.

Hence, the option D is correct, the position of the mailbox is 12 m.

Answer 2

a. The mail carrier's position at
`\(t = 2\) seconds is \(4 \, \text{m}\)`.

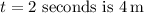b. The position remains at
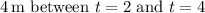`\(4 \, \text{m}\) between \(t = 2\) and \(t = 4\)` seconds.

c. At t = 6 seconds, the mail carrier returns to the initial position at
`\(0 \, \text{m}\)`.

d. The position stays at
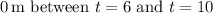`\(0 \, \text{m}\) between \(t = 6\) and \(t = 10\)` seconds.

From the velocity vs. time graph, we can determine the position vs. time graph by integrating the velocity function.

Given the velocity graph:

a. For the first 2 seconds (from 0 to 2 seconds), the velocity is constant at +2 m/s.

`\[ \text{Position} = \text{Initial Position} + \text{Area under the velocity-time graph}\]`

The area under the velocity-time graph during this period (a rectangle) is the velocity (+2 m/s) multiplied by the time interval (2 seconds).

`\[ \text{Area} = \text{Velocity} * \text{Time} = 2 \, \text{m/s} * 2 \, \text{s} = 4 \, \text{m}\]`

Therefore, the position at t = 2 seconds is
`\(4 \, \text{m}\).`

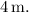
b. For the next 2 seconds (from 2 to 4 seconds), the velocity is
`\(0 \, \text{m/s}\).`

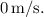
During this interval, the mail carrier remains stationary; hence, the position does not change from
`\(4 \, \text{m}\)`.

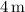c. For the next 2 seconds (from 4 to 6 seconds), the velocity is
`\(-2 \, \text{m/s}\)`.

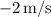The area under the velocity-time graph during this period (a rectangle below the time axis) is the velocity
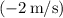`(\(-2 \, \text{m/s}\))` multiplied by the time interval (2 seconds).

`\[ \text{Area} = \text{Velocity} * \text{Time} = -2 \, \text{m/s} * 2 \, \text{s} = -4 \, \text{m}\]`

Since the velocity is negative, it means the mail carrier is moving in the negative direction, which implies a decrease in position.

Therefore, at t = 6 seconds, the position is
`\(4 \, \text{m} - 4 \, \text{m} = 0 \, \text{m}\)`.

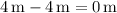d. For the next 4 seconds (from 6 to 10 seconds), the velocity remains 0 m/s.

During this interval, the mail carrier remains stationary; hence, the position stays at 0 m.

Therefore, based on the position vs. time graph, the position of the mailbox is at 0 m (Option A).