Question

I found out the angular speed, but how do i find out the time period or the numbe of revolutions?

Answer 1

Step-by-step explanation:

The problem is asking for the number of revolutions per minute (in other words, the angular speed). If you've found the angular speed in radians per second, you only need to convert your answer to revolutions per minute.

`\omega ((rad)/(s)) * (1\ rev)/(2\pi\ rad) * (60\ s)/(1\ min) = \omega ((rev)/(min) )`

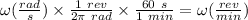
To calculate the angular velocity, first draw a free body diagram of the mass. There are three forces acting on the mass:

Normal force N pushing up,

Weight force mg pulling down,

Friction force F pushing towards the center.

Sum of forces in the centripetal direction:

∑F = ma

F = m v² / r

0.72 W = m v² / r

0.72 mg = m v² / r

0.72 g = v² / r

0.72 g = ω² r

ω = √(0.72 g / r)

Plug in values:

ω = √(0.72 × 9.8 m/s² / 0.35 m)

ω = 4.49 rad/s

ω = 42.9 rev/min

Rounded to two significant figures, the maximum angular velocity is 43 rev/min.