Question

"Find the values of y for which the following is true. The value of the fraction 7-2y-/6 is greater than the value of the fraction -Зу 7/12"

Answer 1

The values of y for which the inequality
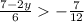`\( (7 - 2y)/(6) > -(7)/(12) \)` is true are
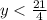`\( y < (21)/(4) \)`, or in decimal form,
`\( y < 5.25 \)`.

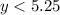To find the values of y for which the fraction
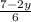`\( (7 - 2y)/(6) \)` is greater than the fraction
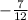`\( -(7)/(12) \)`, we can set up the following inequality:

`\[ (7 - 2y)/(6) > -(7)/(12) \]`

Now, let's solve this inequality step by step:

Step 1: Multiply both sides of the inequality by 12 to get rid of the fractions:

`\[ 12 \left((7 - 2y)/(6)\right) > 12 \left(-(7)/(12)\right) \]`

Simplify:

`\[ 2(7 - 2y) > -7 \]`

Step 2: Distribute the 2 on the left side of the inequality:

`\[ 14 - 4y > -7 \]`

Step 3: Add 7 to both sides to isolate the term with y on the left side:

`\[ 14 - 4y + 7 > 0 \]`

Simplify:

`\[ 21 - 4y > 0 \]`

Step 4: Subtract 21 from both sides:

`\[ -4y > -21 \]`

Step 5: Divide both sides by -4, remembering to reverse the inequality since we are dividing by a negative number:

`\[ y < (21)/(4) \]`

So, The answer is
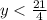`\( y < (21)/(4) \)`, or in decimal form,
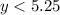`\( y < 5.25 \)`.

Answer 2

The values for which the expression is true is y<3.

How to solve inequality problem.

In mathematics, inequality represents a relation between two expressions, indicating that one is greater than, less than, or not equal to the other.

Symbols like <, >, ≤, and ≥ are used.

Given

`(7 - 2y)/(6) > (3y - 7)/(12)`

Multiply through with LCM 12

`12( (7 - 2y)/(6)) > ((3y - 7)/(12) )12`

2(7-2y) > 3y-7

Expand

14-4y>3y-7

14+7>3y+4y

21>7y

21/7>y

3>y

y<3

The values for which the expression is true is y<3.

Complete question

"Find the values of y for which the following is true. The value of the fraction

`(7 - 2y)/(6) is greater than the value of the fraction (3y - 7)/(12)`