Question

A certain virus infects one in every 500 people. A test used to detect the virus in a person is positive 80% of the time if the person has the virus and 8% of the time if the person does not have the virus. (This 8% result is called a false positive.) Let A be the event "the person is infected" and B be the event "the person tests positive' a Find the probability that a person has the virus given that they have tested positive: find P(VI+). Round your answer to 2 decimal places P(V|+)= 80 b) Find the probability that a person does not have the virus given that they test negative: find P(V' I-). Round your answer to 2 decimal places P(V'|-) =

Answer 1

The probability that a person has the virus given that they have tested positive is approximately 0.0198. the probability that a person does not have the virus given that they test negative is approximately 0.9996.

Let's use conditional probability to find the probabilities in each case:

a) Probability that a person has the virus given that they have tested positive (P(A|B)):

`P(A \mid B)=(P(B \mid A) \cdot P(A))/(P(B \mid A) \cdot P(A)+P\left(B \mid A^(\prime)\right) \cdot P\left(A^(\prime)\right))`

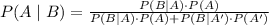
Given:

P(A)= 1/500 (Probability that a person has the virus)

P(B∣A)=0.80 (Probability of testing positive given the person has the virus)

P(B∣A')=0.08 (Probability of testing positive given the person does not have the virus)

P(A')=1−P(A) (Probability that a person does not have the virus)

Now plug these values into the formula:

`P(A \mid B)=((0.80) \cdot (1)/(500))/((0.80) \cdot (1)/(500)+(0.08) \cdot (499)/(500))`

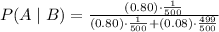
Calculating:

`P(A \mid B)=(0.0008)/(0.0008+0.0396)`

`P(A \mid B) \approx (0.0008)/(0.0404)`

`P(A \mid B) \approx 0.0198\\`

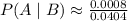
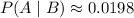
So, the likelihood of an individual having the virus, given a positive test result, is approximately 0.0198 (rounded to the nearest hundredth of a percent).

b) Probability that a person does not have the virus given that they test negative (P(not A | not B)):

`P(not A \mid not B)=(P(notB \mid notA) \cdot P(notA))/(P(notB \mid notA) \cdot P(notA)+P\left(notB \mid A\right) \cdot P\left(A\right))`

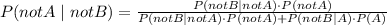
Given:

P(not B ∣ not A)=0.92 (Probability of testing negative given the person does not have the virus)

P(not B∣A)=1−P(B∣A) (Probability of testing negative given the person has the virus)

Now plug in the values:

`P(not A \mid not B)=((0.92) \cdot (499)/(500))/((0.92) \cdot (499)/(500)+(1-0.80) \cdot (1)/(500))`

`P(not A \mid not B)=(0.91736)/(0.0004+0.91736)`

`P(not A \mid not B) \approx (0.91736)/(0.91776)`

`P(not A \mid not B) \approx 0.9996`

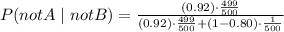
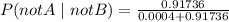
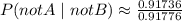
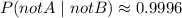
So, the likelihood of an individual being free of the virus, given a negative test result, is approximately 0.9996 (rounded to the nearest hundredth of a percent).

Complete Question:

A certain virus infects one in every 500 people. A test used to detect the virus in a person is positive 80% of the time if the person has the virus and positive 8% of the time if the person does not have the virus. (This 8% result is called a false positive.) Let A be the event "the person is infected" and B be the event "the person tests positive".

a. Find the probability that a person has the virus given that they have tested positive, i.e. find P(A if B). Round your answer to the nearest hundredth of a percent and do not include a percent sign. P(A if B)= % b.

b. Find the probability that a person does not have the virus given that they test negative, i.e. find P( not A if not B). Round your answer to the nearest hundredth of a percent and do not include a percent sign. P(not A if not B)=