Answer:
 different playlists are possible
different playlists are possible
Explanation:
The order in which the songs are played is not important, which means that the combinations formula is used to solve this question.
Combinations formula:
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.
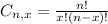
In this question:
6 songs, so 2 reggae(from a set of 5), 2 hip hop(from a set of 15) and 2 blues(from a set of 13). So
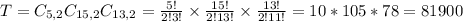
In scientific notations:
4 digits after the first, which is 8, so:
 different playlists are possible
different playlists are possible