Question

DJ Kenisha is making a playlist for a radio show; she is trying to decide what 6 songs to play and in what order they should be played. If she has her choices narrowed down to 5 reggae, 15 hip-hop, and 13 blues songs, and she wants to play an equal number of reggae, hip-hop, and blues songs, how many different playlists are possible? Express your answer in scientific notation rounding to the hundredths place.

Answer 1

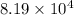`8.19 * 10^(4)` different playlists are possible

Explanation:

The order in which the songs are played is not important, which means that the combinations formula is used to solve this question.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

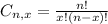
In this question:

6 songs, so 2 reggae(from a set of 5), 2 hip hop(from a set of 15) and 2 blues(from a set of 13). So

`T = C_(5,2)C_(15,2)C_(13,2) = (5!)/(2!3!) * (15!)/(2!13!) * (13!)/(2!11!) = 10*105*78 = 81900`

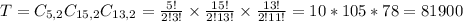
In scientific notations:

4 digits after the first, which is 8, so:

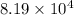`8.19 * 10^(4)` different playlists are possible