The line
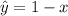 is the better fit for the data based on the least-squares criterion because it has the smaller sum of squared residuals.
is the better fit for the data based on the least-squares criterion because it has the smaller sum of squared residuals.
The predicted values
 for each x using the equation
for each x using the equation
 are:
are:
For
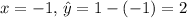
For
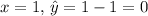
For
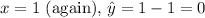
For

For x = 5,
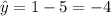
The squared residuals for the first line equation
 are:
are:
For x = -1, residual squared is
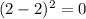
For x = 1, residual squared is

For x = 1 (again), residual squared is
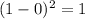
For x = 3, residual squared is
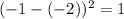
For x = 5, residual squared is
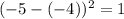
The sum of the squared residuals for the first line equation
 is 0 + 0 + 1 + 1 + 1 = 3.
is 0 + 0 + 1 + 1 + 1 = 3.
predicted values
 for each x using the equation
for each x using the equation
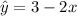 are:
are:
For
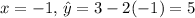
For
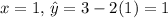
For
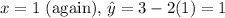
For
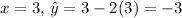
For

The squared residuals for the second line equation
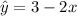 are:
are:
For x = -1, residual squared is
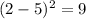
For x = 1, residual squared is
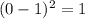
For x = 1 (again), residual squared is
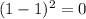
For x = 3, residual squared is
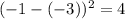
For x = 5, residual squared is
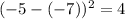
The sum of the squared residuals for the second line equation
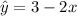 is 9 + 1 + 0 + 4 + 4 = 18.
is 9 + 1 + 0 + 4 + 4 = 18.
The sum of squared residuals for the first line equation
 is smaller (3) than the sum for the second line equation
is smaller (3) than the sum for the second line equation
 , so the line
, so the line
 better fits the data according to the least-squares criterion.
better fits the data according to the least-squares criterion.